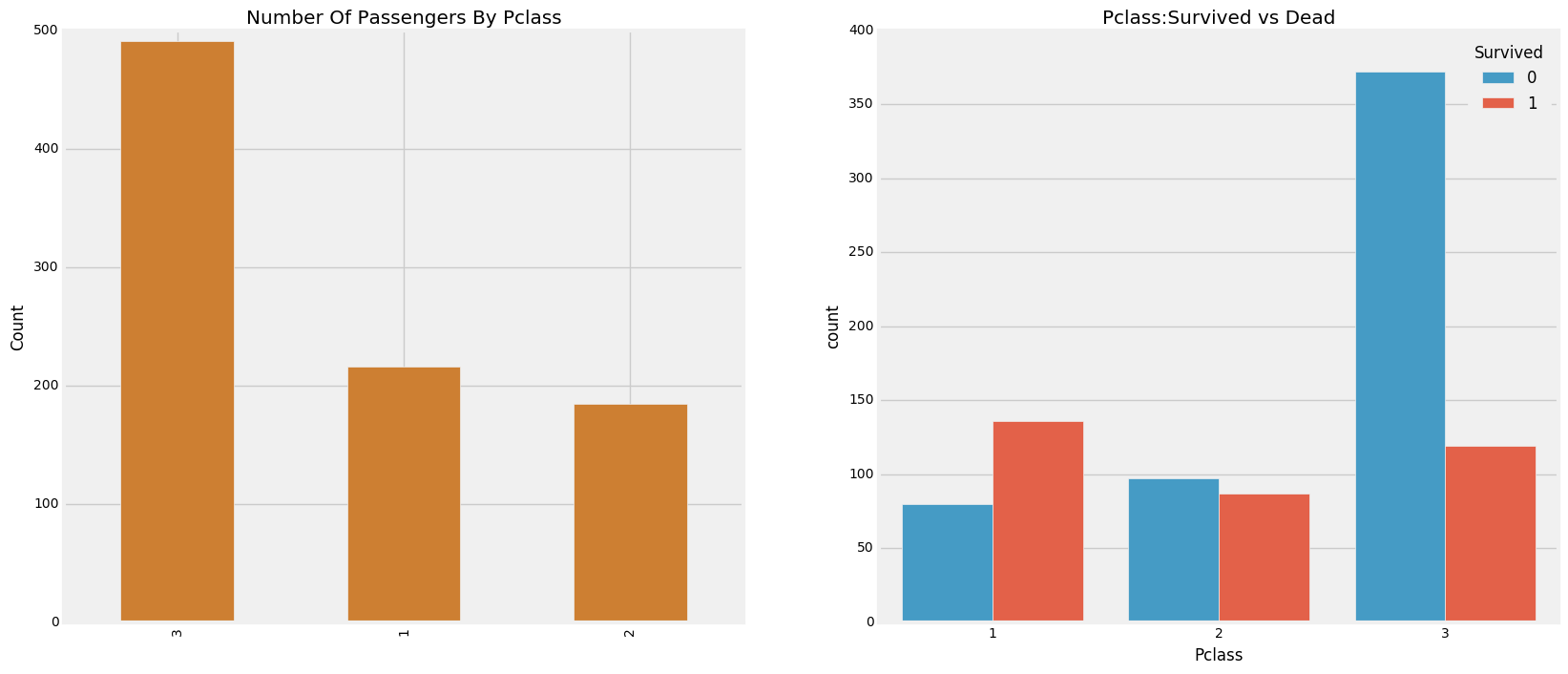泰坦尼克号乘客生存预测

案例背景

泰坦尼克号沉船事故是世界上最著名的沉船事故之一。1912年4月15日，在她的处女航期间，泰坦尼克号撞上冰山后沉没，造成2224名乘客和机组人员中超过1502人的死亡。这一轰动的悲剧震惊了国际社会，并导致更好的船舶安全法规。 事故中导致死亡的一个原因是许多船员和乘客没有足够的救生艇。然而在被获救群体中也有一些比较幸运的因素；一些人群在事故中被救的几率高于其他人，比如妇女、儿童和上层阶级。 这个Case里，我们需要分析和判断出什么样的人更容易获救。最重要的是，要利用机器学习来预测出在这场灾难中哪些人会最终获救；

---

数据挖掘流程

(一)数据读取

• 读取数据，并进行展示
• 统计数据各项指标
• 明确数据规模与要完成的任务

(二)特征理解分析

• 单特征分析，逐个变量分析其对结果的影响
• 多变量统计分析，综合考虑多种情况影响
• 统计绘图得出结论

(三)数据清洗与预处理

• 对缺失值进行填充
• 特征标准化/归一化
• 筛选有价值的特征
• 分析特征之间的相关性

(四)建立模型

• 特征数据与标签准备
• 数据集切分
• 多种建模算法对比
• 集成策略等方案改进

---

数据样本

此项目数据集分为2份数据集：titanic_train.csv和titanic_test.csv

titanic_train.csv: 训练集，共计891条数据 titanic_test.csv: 测试集，共计418条数据

---

数据特征

字段	字段说明
PassengerId	乘客编号
Survived	存活情况(存活:1; 死亡:0)
Pclass	客舱等级
Name	乘客姓名
Sex	性别
Age	年龄
SibSp	同乘的兄弟姐妹/配偶数
Parch	同乘的父母/小孩数
Ticket	船票编号
Fare	船票价格
Cabin	客舱号
Embarked	登船港口

PassengerId是数据唯一序号；Survived是存活情况，为预测标记特征；剩下的10个是原始特征数据。

---

数据统计与统计分析

• 查看哪些列有缺失值？

属性	数目
PassengerId	0
Survived	0
Pclass	0
Name	0
Sex	0
Age	177
SibSp	0
Parch	0
Ticket	0
Fare	0
Cabin	687
Embarked	2

从上面可以看出来Cabin这个属性缺失值比较多

• 整体看看数据啥规模？(利用Pandas的describe()函数)

PassengerId	Survived	Pclass	Age	SibSp	Parch	Fare
count	891.000000	891.000000	891.000000	714.000000	891.000000	891.000000
mean	446.000000	0.383838	2.308642	29.699118	0.523008	0.381594
std	257.353842	0.486592	0.836071	14.526497	1.102743	0.806057
min	1.000000	0.000000	1.000000	0.420000	0.000000	0.000000
25%	223.500000	0.000000	2.000000	20.125000	0.000000	0.000000
50%	446.000000	0.000000	3.000000	28.000000	0.000000	0.000000
75%	668.500000	1.000000	3.000000	38.000000	1.000000	0.000000
max	891.000000	1.000000	3.000000	80.000000	8.000000	6.000000

mean字段告诉我们，大概0.383838的人最后获救了，2/3等舱的人数比1等舱要多，平均乘客年龄大概是29.7岁(计算这个时候会略掉无记录的)等等…

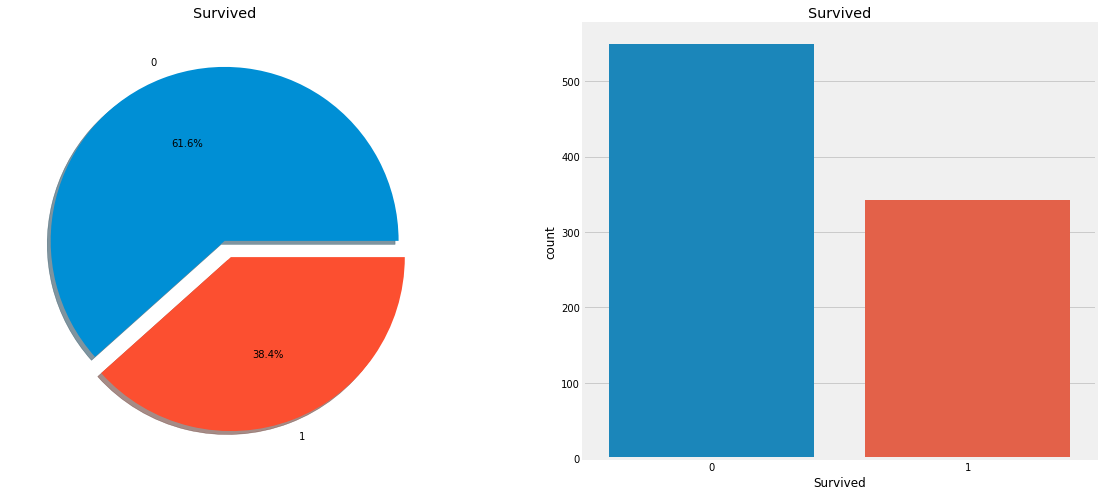
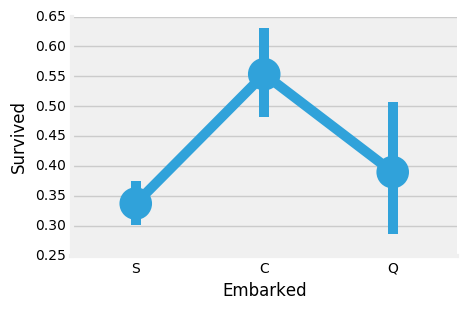
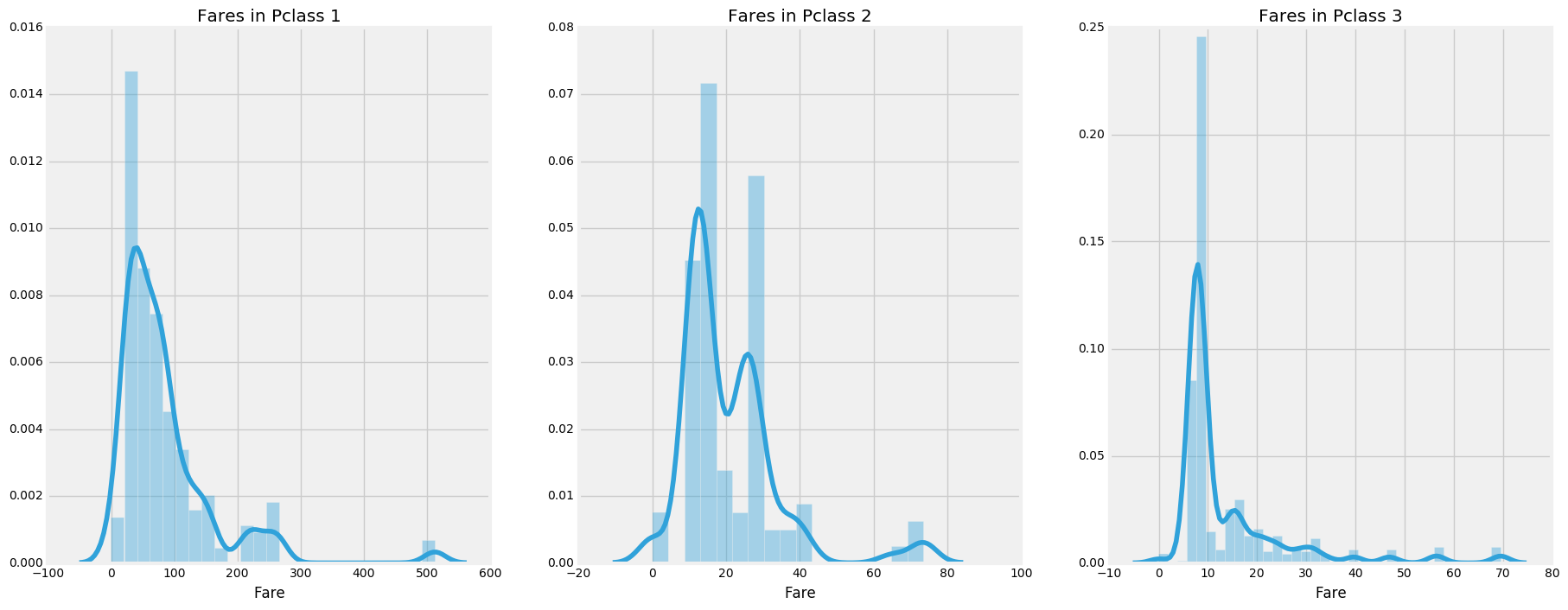
• 通过绘图来看看获救比例咋样

---

性别特征分析

数据特征分为：连续值和离散值

• 离散值：性别(男、女)，登船地点(S, Q, C)
• 连续值：年龄，船票价格

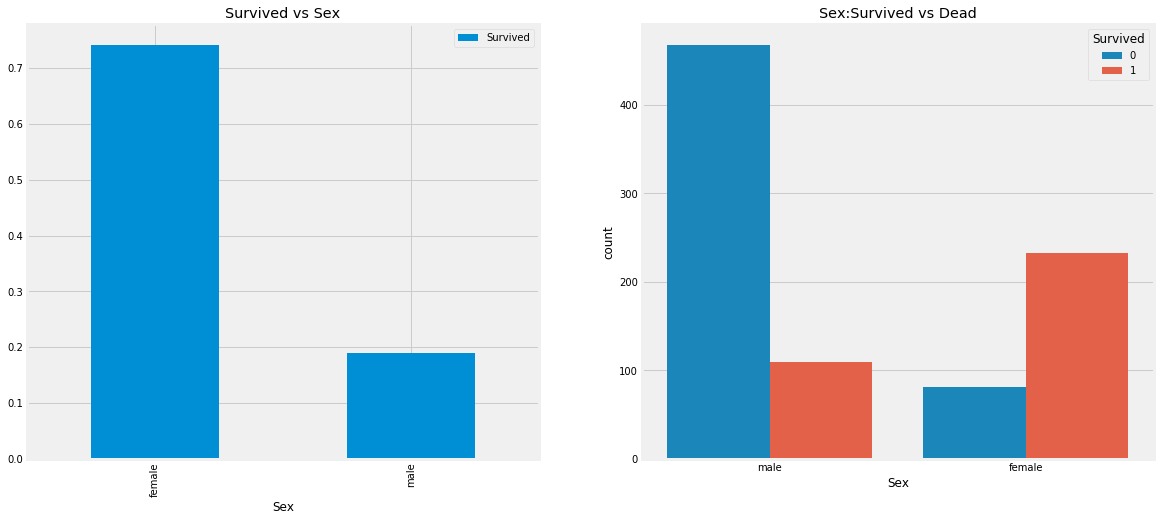
按照性别进行分组分别输出获救人数：

Sex	Survived	Sum
female	0	81
female	1	233
male	0	468
male	1	109

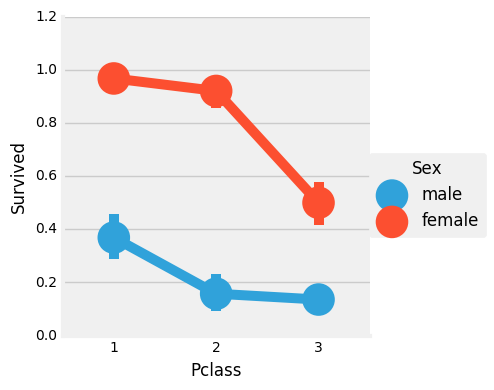
画出相应的图如下所示：

---

船舱等级特征分析

Survivied	0	1	All
Pclass
1	80	136	216
2	97	87	184
3	372	119	491
All	549	342	891

我们可以清楚地看到，船舱等级为1的被给予很高的优先级而救援。尽管数量在Pclass3乘客高了很多，仍然存活数从他们是非常低的，大约25%

对于Pclass1来说存活是63%左右，而Pclass2大约是48%。所以金钱和地位很重要。这样一个物欲横流的世界。

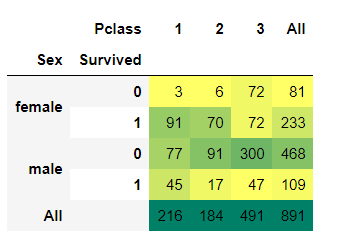
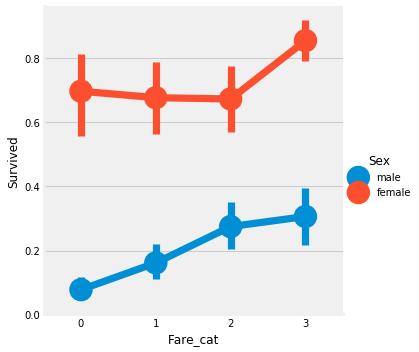
那这些又和性别有关吗？接下来我们再来看看船舱等级和性别对结果的影响。(多变量分析)

我们可以很容易地推断，从Pclass1女性生存是95-96%，如94人中只有3位女性从Pclass1没获救。

显而易见的是，不论Pclass，女性优先考虑。

看来Pclass也是一个重要的特征。让我们分析其他特征。

---

年龄特征缺失值填充与分析(连续值)

• Oldest Passenger was of: 80.0 Years
• Youngest Passenger was of: 0.42 Years
• Average Age on the ship: 29.69911764705882 Years

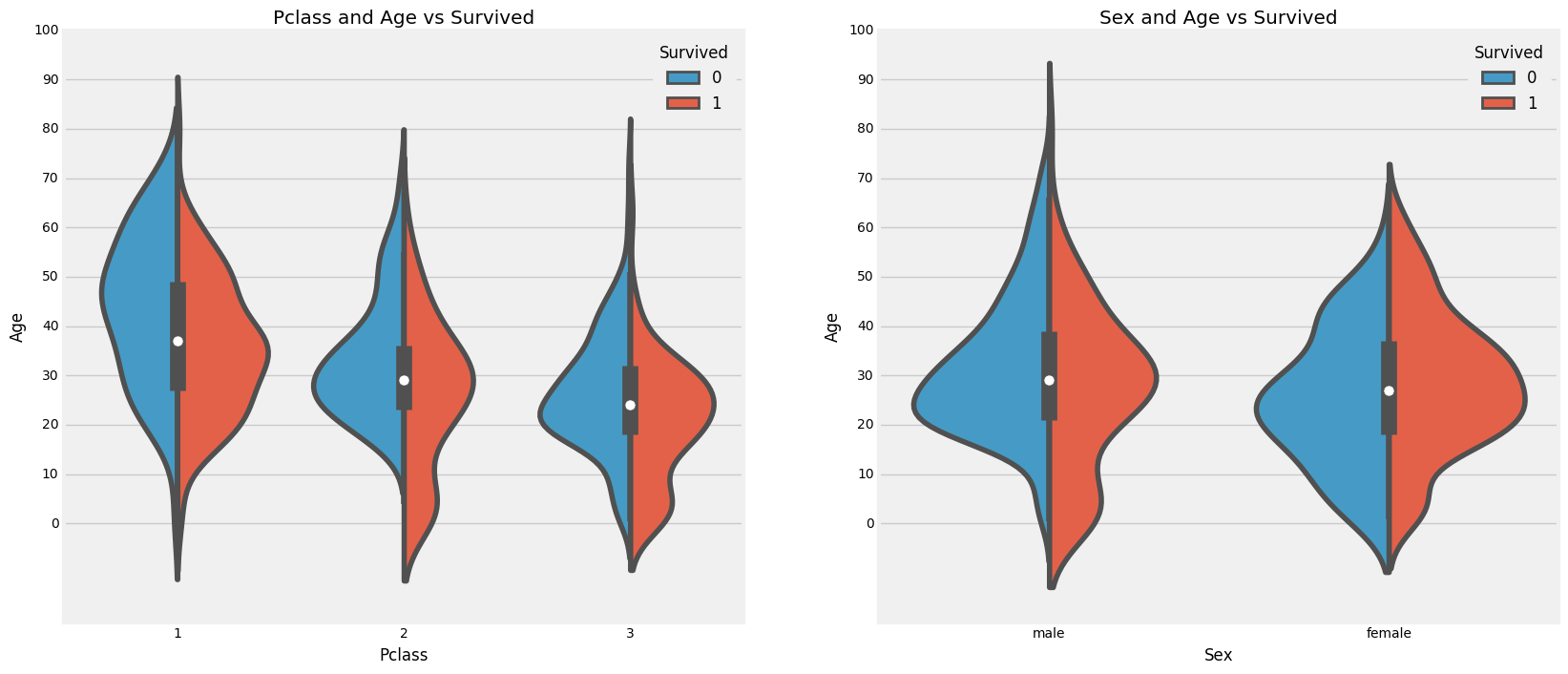
可以得出以下结论：

• 10岁以下儿童的存活率随passenegers数量增加；
• 生存为20-50岁获救几率更高一些；
• 对男性来说，随着年龄的增长，存活率降低

缺失值填充

• 平均值
• 经验值
• 回归模型预测
• 剔除掉

正如我们前面看到的，年龄特征有177个空值。为了替换这些缺失值，我们可以给它们分配数据集的平均年龄。

但问题是，有许多不同年龄的人。最好的办法是找到一个合适的年龄段！

我们可以检查名字特征。根据这个特征，我们可以看到名字有像先生或夫人这样的称呼，这样我们就可以把先生和夫人的平均值分配给各自的组。

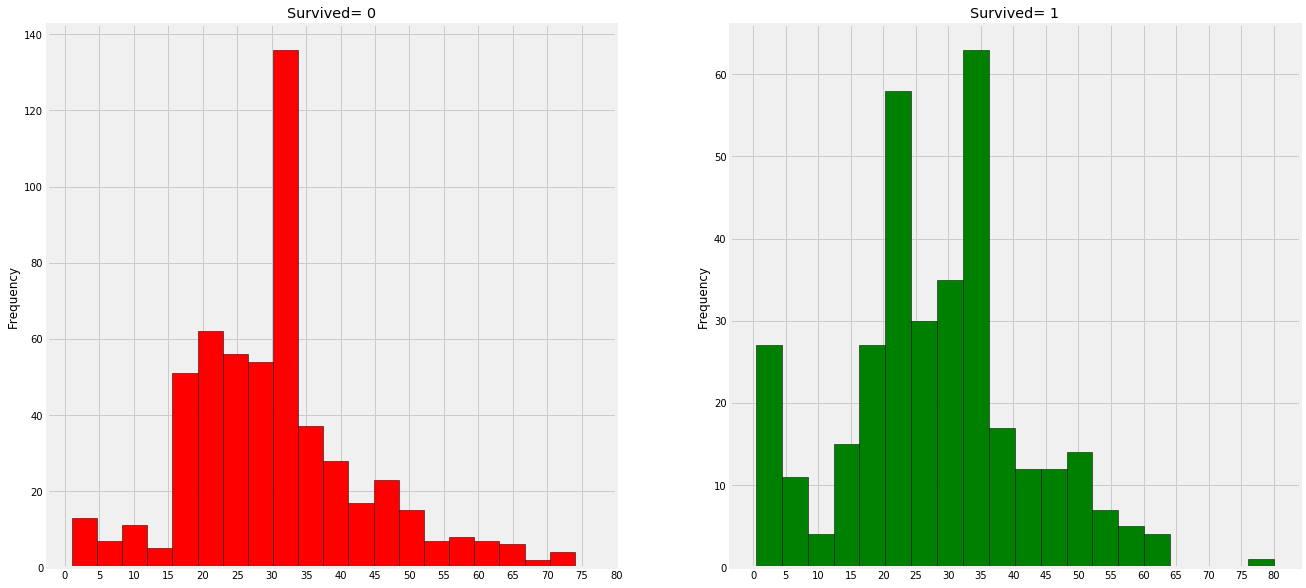
观察：

• 幼儿(年龄在5岁以下(获救的还是蛮多的(妇女和儿童优先政策)
• 最老的乘客得救了(80年)
• 死亡人数最高的是30-40岁年龄组

---

登船地点特征分析

C港生存的可能性最高在0.55左右，而S的生存率最低。

观察:

• 大部分人的船舱等级是3
• C的乘客看起来很幸运，他们中的一部分幸存下来
• S港口的富人蛮多的。仍然生存的机会很低
• 港口Q几乎有95%的乘客都是穷人

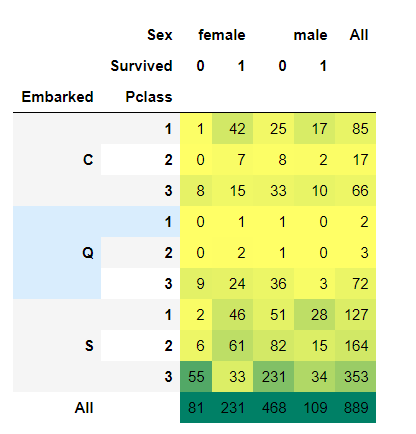
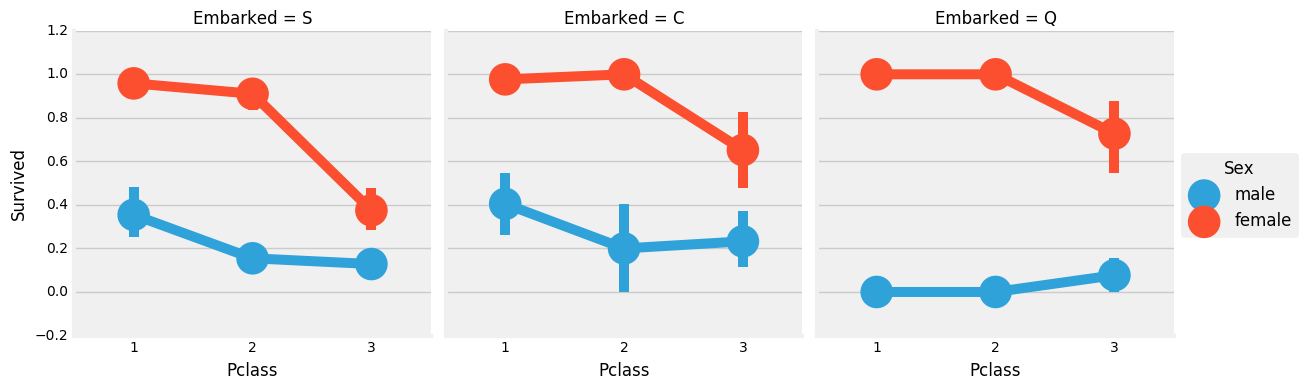
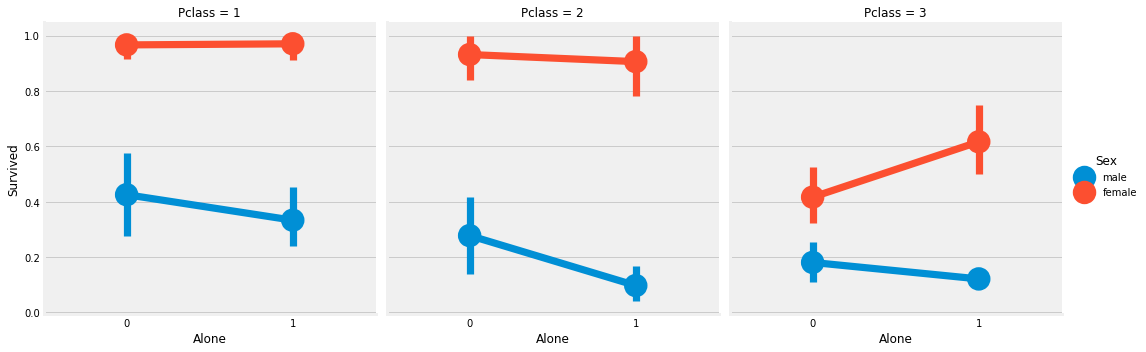
观察:

• 存活的几率几乎为1, 在Pclass1和Pclass2中的女人
• Pclass3的乘客中男性和女性的生存率都是很偏低的
• 港口Q很不幸，因为那里都是3等舱的乘客

Note:

港口中也存在缺失值，在这里用众数来进行填充了，因为S登船人最多呀

---

家庭特征分析

兄弟姐妹的数量

• 这个特征表示一个人是独自一人还是与他的家人在一起

Survived	0	1
SibSp
0	398	210
1	97	112
2	15	13
3	12	4
4	15	3
5	5	0
8	7	0

Pclass	1	2	3
SibSp
0	137	120	351
1	71	55	83
2	5	8	15
3	3	1	12
4	0	0	18
5	0	0	5
8	0	0	7

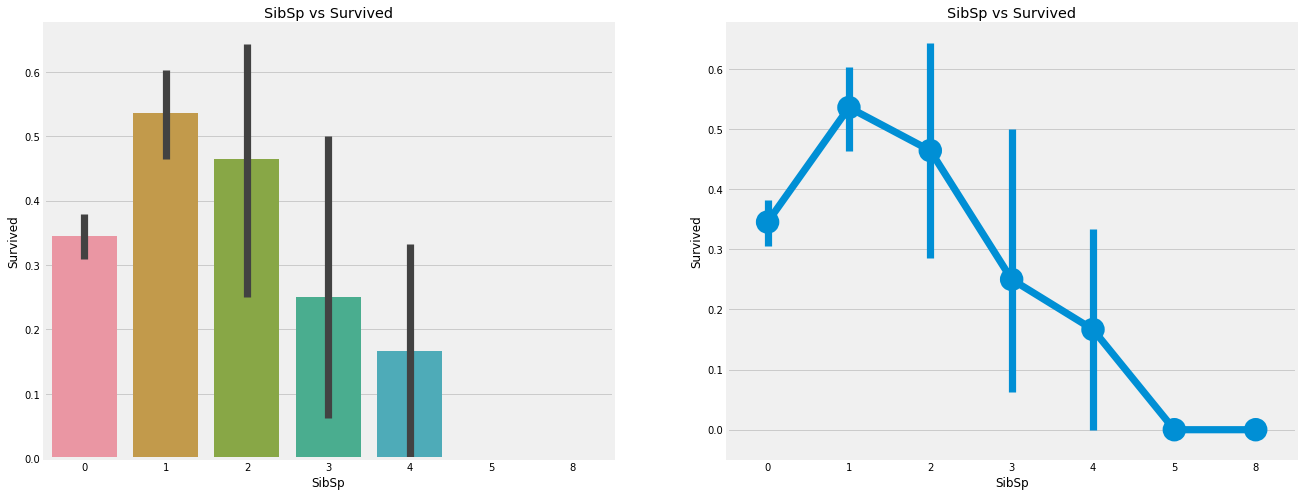
观察：

如果乘客是孤独的船上没有兄弟姐妹，他有34.5%的存活率。如果兄弟姐妹的数量增加，概率大致减少。这是有道理的。也就是说，如果我有一个家庭在船上，我会尽力拯救他们，而不是先救自己。但是令人惊讶的是，5-8名成员家庭的存活率为0%。原因可能是他们在pclass=3的船舱？

父母和孩子的数量

Pclass	1	2	3
Parch
0	163	134	381
1	31	32	55
2	21	16	43
3	0	2	3
4	1	0	3
5	0	0	5
6	0	0	1

以上再次表明，大家庭都在Pclass3

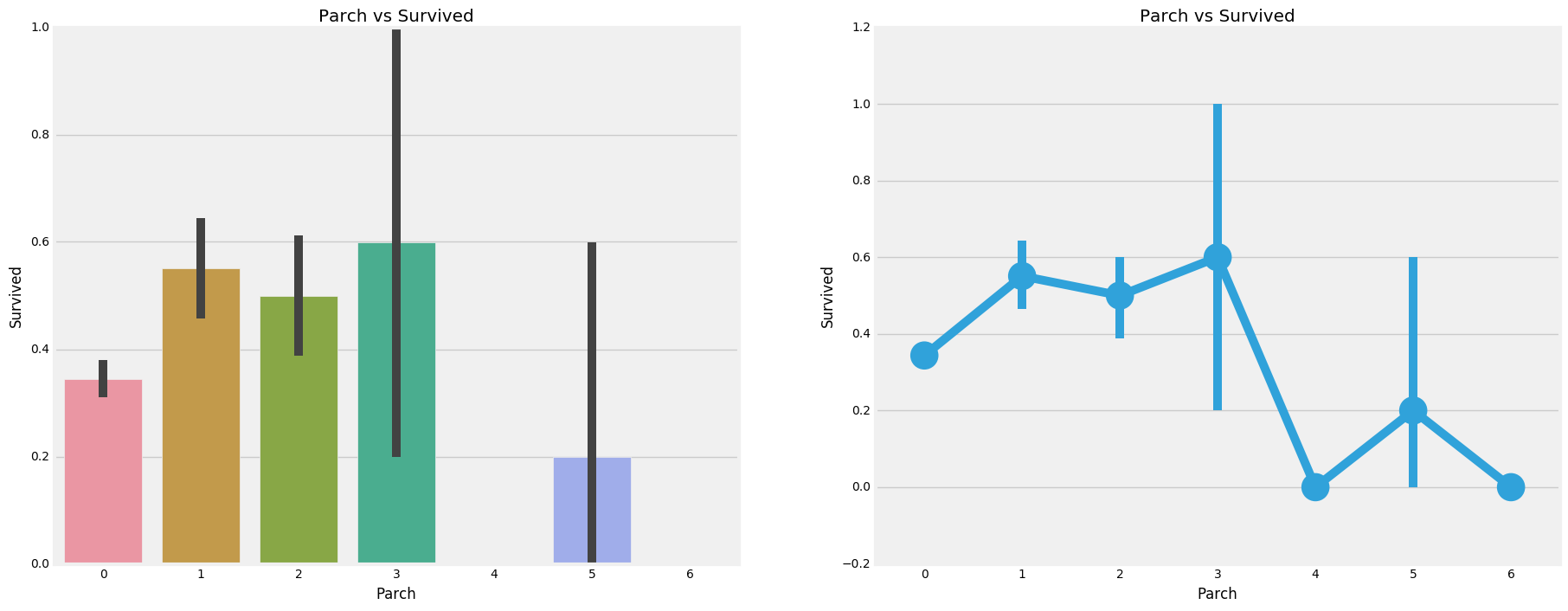
观察：

这里的结果也很相似。带着父母的乘客有更大的生存机会。然而，它随着数字的增加而减少。

在船上的家庭父母人数中有1-3个的人的生存机会是好的。独自一人也证明是致命的，当船上有4个父母时，生存的机会就会减少。

---

船票的价格特征分析

• Highest Fare was: 512.3292
• Lowest Fare was: 0.0
• Average Fare was: 32.204207968574636

---

特征相关性

概括地观察所有的特征:

• 性别：与男性相比，女性的生存机会很高
• Pclass：有第一类乘客给你更好的生存机会的一个明显趋势。对于Pclass3成活率很低。对于女性来说，从Pclass1生存的机会几乎是100%
• 年龄：小于5-10岁的儿童存活率高。年龄在15到35岁之间的乘客死亡很多
• 港口：上来的仓位也有区别，死亡率也很大！
• 家庭：有1-2的兄弟姐妹、配偶或加上父母有1-3人, 而不是独自一人或有一个大家庭旅行，你有更大的概率存活下来。

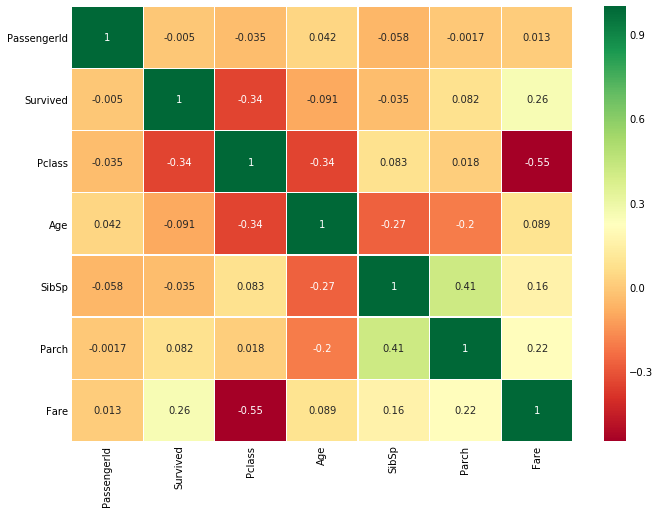
首先要注意的是，只有数值特征进行比较

正相关：如果特征A的增加导致特征B的增加，那么它们呈正相关。值1表示完全正相关。

负相关：如果特征A的增加导致特征B的减少，则呈负相关。值-1表示完全负相关。

现在让我们说两个特性是高度或完全相关的，所以一个增加导致另一个增加。这意味着两个特征都包含高度相似的信息，并且信息很少或没有变化。这样的特征对我们来说是没有价值的！

那么你认为我们应该同时使用它们吗？。在制作或训练模型时，我们应该尽量减少冗余特性，因为它减少了训练时间和许多优点。

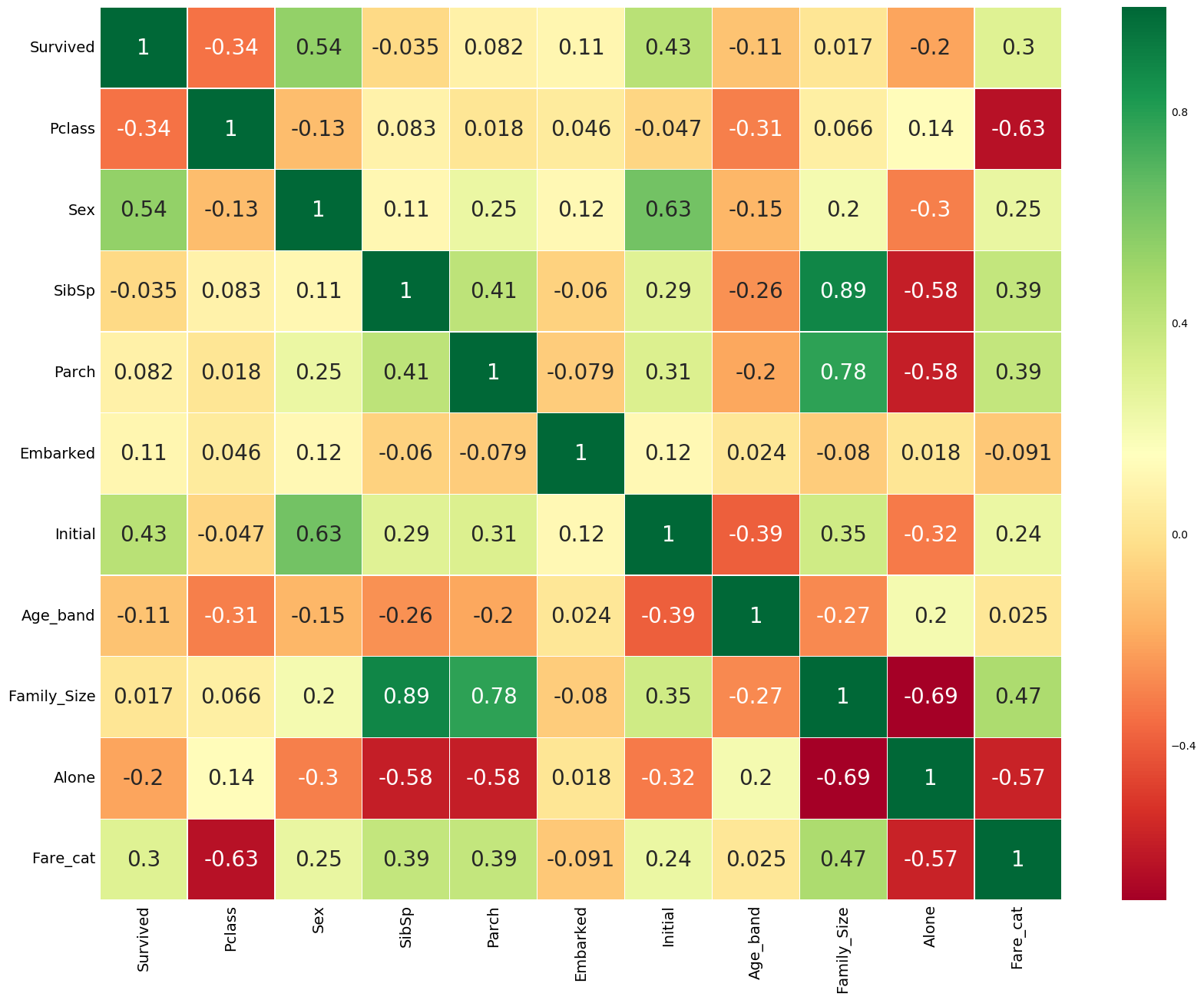
现在，从上面的图，我们可以看到，特征不显著相关。

---

特征工程和数据清洗

当我们得到一个具有特征的数据集时，是不是所有的特性都很重要？可能有许多冗余的特征应该被消除，我们还可以通过观察或从其他特征中提取信息来获得或添加新特性。

• 连续特征离散化(年龄)

年龄的取值范围是[0, 80], 我们将其分为5组。

Age_band	Sum
1	382
2	325
0	104
3	69
4	11

Note: 0表示0-16岁，1表示17-32岁，2表示33-48岁，3表示49-64岁，5表示65-80岁

从上图可以看出：生存率随年龄的增加而减少，不论Pclass。

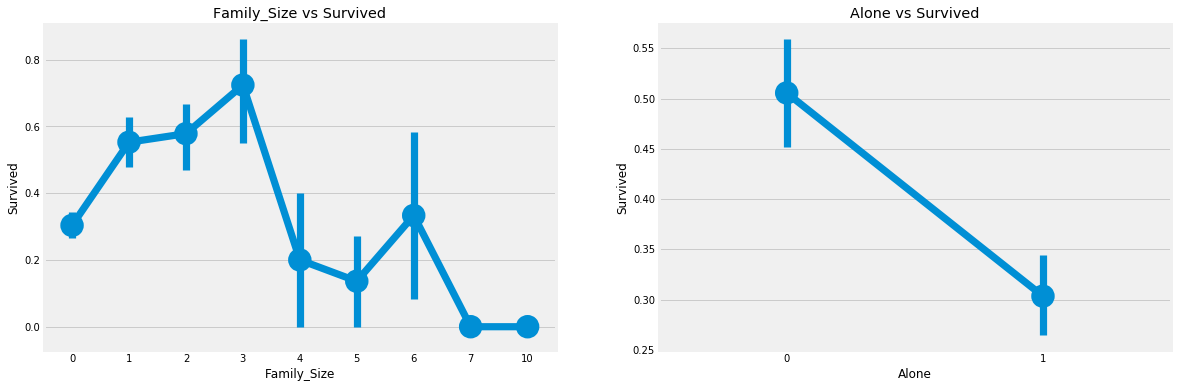
• Family_size：家庭总人数

光看兄弟姐妹和老人孩子看感觉不太直接，这里我们直接看全家的人数

从上图可以看出：Family_size = 0意味着passeneger是孤独的。显然，如果你是单独或family_size = 0，那么生存的机会很低。家庭规模4以上，机会也减少。这看起来也是模型的一个重要特性。让我们进一步研究这个问题

• 连续特征离散化(船票价格)

因为票价也是连续的特性，所以我们需要将它离散化

Survived	Fare_Range
(-0.001, 7.91]	0.197309
(7.91, 14.454]	0.303571
(14.454, 31.0]	0.454955
(31.0, 512.329]	0.581081

如上所述，我们可以清楚地看到，船票价格增加生存的机会增加.

显然，随着fare_cat增加，存活的几率增加。随着性别的变化，这一特性可能成为建模过程中的一个重要特征。

总结：

• 去掉一些不必要的特征：

  • 乘客姓名 ---> 我们不需要name特性，因为它不能转换成任何分类值
  • 年龄 ---> 我们有age_band特征，所以不需要这个年龄特征
  • 船票编号 ---> 这是任意的字符串，不能被归类
  • 船票价格 ---> 我们有fare_cat特征，所以不需要船票价格特征
  • 客仓号 ---> 这个也不需要，因为没啥含义
  • 乘客编号 ---> 不能被归类

• 我们再来看看去掉部分无用特征后的特征之间的关系图：

现在我们再看以上的相关图，我们可以看到一些正相关的特征。

---

机器学习建模

我们从EDA部分获得了一些见解。但是，我们不能准确地预测或判断一个乘客是否会幸存或死亡。现在我们将使用一些很好的分类算法来预测乘客是否能生存下来：

• Logistic回归
• 支持向量机(线性和径向)
• 随机森林
• k-近邻
• 朴素贝叶斯
• 决策树
• 神经网络

以下是这些模型单个的预测结果：

无特殊声明，均使用默认参数

• Radial Support Vector Machines(rbf-SVM)

  • Accuracy for rbf SVM is 0.835820895522388

• Linear Support Vector Machine(linear-SVM)

  • Accuracy for linear SVM is 0.8171641791044776

• Logistic Regression

  • The accuracy of the Logistic Regression is 0.8171641791044776

• Decision Tree

  • The accuracy of the Decision Tree is 0.7985074626865671

• K-Nearest Neighbours(KNN)

  • The accuracy of the KNN is 0.832089552238806

• Naive Bayes

  • The accuracy of the NaiveBayes is 0.8134328358208955

• Random Forest

  • The accuracy of the Random Forests is 0.8097014925373134

模型的精度并不是决定分类器效果的唯一因素。假设分类器在训练数据上进行训练，需要在测试集上进行测试才有效果

现在这个分类器的精确度很高，但是我们可以确认所有的新测试集都是90%吗？答案是否定的，因为我们不能确定分类器在不同数据源上的结果。当训练和测试数据发生变化时，精确度也会改变。它可能会增加或减少

为了克服这一点，得到一个广义模型，我们使用交叉验证

---

交叉验证

一个测试集看起来不太够呀，多轮求均值是一个好的策略.

• 交叉验证的工作原理是首先将数据集分成k-subsets(K个大小相似的互斥子集)
• 假设我们将数据集划分为（k＝5）部分。我们预留1个部分进行测试，并对其他4个部分进行训练
• 我们通过在每次迭代中改变测试部分并在其他部分中训练算法来继续这个过程。然后对衡量结果求平均值，得到算法的平均精度

以上就是所谓的交叉验证

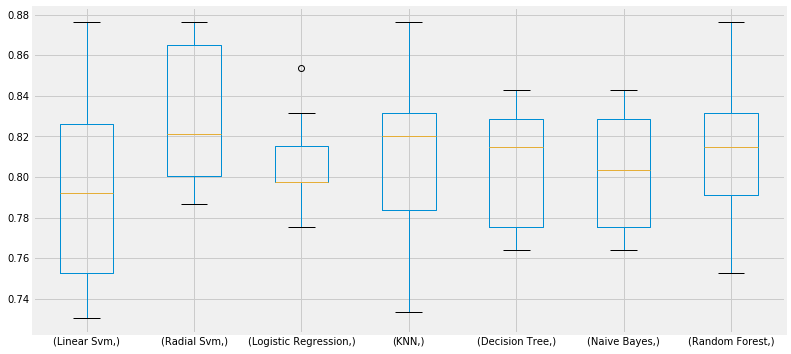
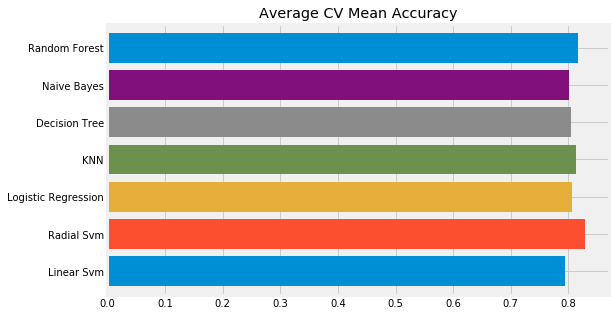
Machine Learning Methods	CV Mean	Std
Linear Svm	0.793471	0.047797
Radial Svm	0.828290	0.034427
Logistic Regression	0.805843	0.021861
KNN	0.813783	0.041210
Decision Tree	0.804757	0.029890
Naive Bayes	0.801386	0.028999
Random Forest	0.815968	0.035414

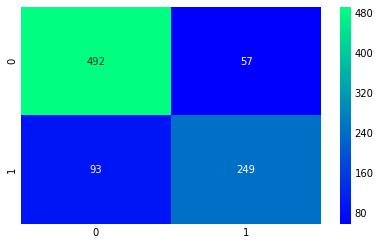
解释混淆矩阵：来看第一个图

• 预测的正确率为491(死亡) + 247(存活)，平均CV准确率为(491+247)/ 891＝82.8%

• 58和95都是我们的算法预测错了的

---

超参数整定

机器学习模型就像一个黑盒子。这个黑盒有一些默认参数值，我们可以调整或更改以获得更好的模型。比如支持向量机模型中的C和γ，我们称之为超参数，他们对结果可能产生非常大的影响

主要是利用网格搜索来选出最优参数

例如，进行网格搜索之后： RBF支持向量机的最佳得分为82.82%，C＝0.5，γ＝0.1。RandomForest，成绩是81.8%

---

集成模块

集成是提高模型的精度和性能的一个很好的方式。简单地说，是各种简单模型的结合创造了一个强大的模型

• Bagging 类似随机森林类型的，并行的集成
• Boosting 提升类型
• Stacking 堆叠类型
• Blending

Bagging

Bagging将多个模型，也就是多个基学习器的预测结果进行简单的加权平均或者投票。它的好处是可以并行地训练基学习器。Random Forest就用到了Bagging的思想。

• Bagging KNN

  • The accuracy for bagged KNN is: 0.835820895522
  • The cross validated score for bagged KNN is: 0.814889342867

• Bagging Decision Tree

  • The accuracy for bagged Decision Tree is: 0.824626865672
  • The cross validated score for bagged Decision Tree is: 0.820482635342

Boosting

Boosting的思想有点像知错能改，每个基学习器是在上一个基学习器学习的基础上，对上一个基学习器的错误进行弥补。我们将会用到的AdaBoost，Gradient Boost就用到了这种思想

提升是一个逐步增强的弱模型，首先对完整的数据集进行训练。现在模型会得到一些实例，而有些错误。现在，在下一次迭代中，学习者将更多地关注错误预测的实例或赋予它更多的权重.

AdaBoost(自适应增强)---在这种情况下，弱学习或估计是一个决策树。但我们可以改变缺省base_estimator任何算法的选择

• Adaboost
  • The cross validated score for AdaBoost is: 0.8249526160481218
  • The cross validated score for Gradient Boosting is: 0.818286233118

Stacking

Stacking是用新的次学习器去学习如何组合上一层的基学习器。如果把Bagging看作是多个基分类器的线性组合，那么Stacking就是多个基分类器的非线性组合。Stacking可以将学习器一层一层地堆砌起来，形成一个网状的结构

相比来说Stacking的融合框架相对前面的二者来说在精度上确实有一定的提升。

Blending

Blending和Stacking很相似，但同时它可以防止信息泄露的问题。

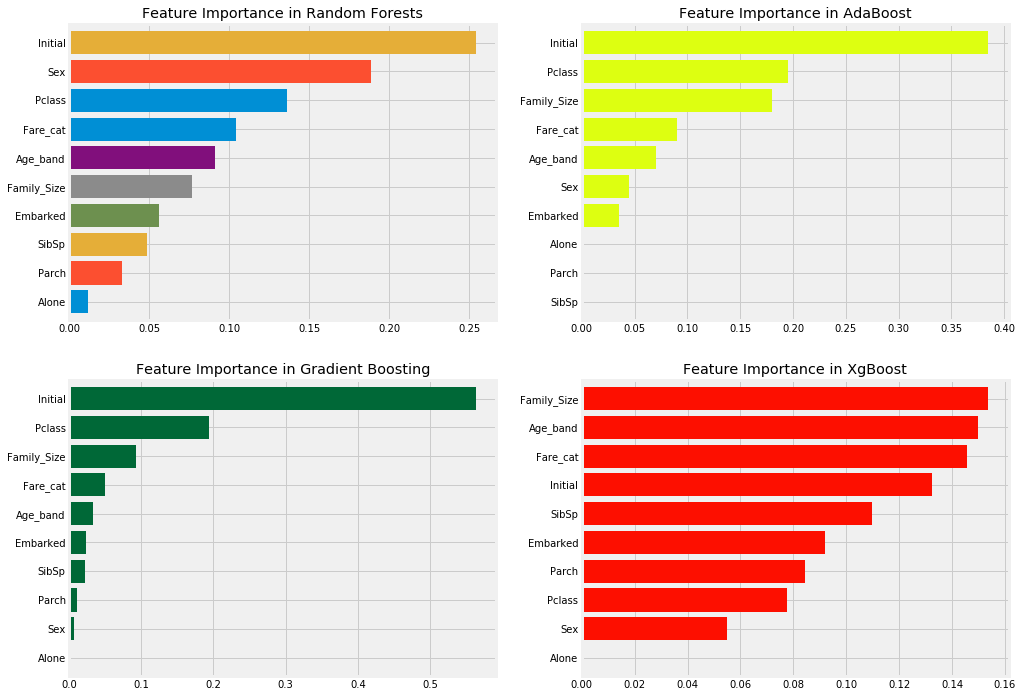
我们得到了最高的精度为AdaBoost。我们将尝试用超参数调整来增加它

我们可以从AdaBoost的最高精度是83.16%，n_estimators = 200和learning_rate = 0.05

Confusion Matrix for the Best Model

---

特征重要性衡量

---

配置环境

• Python 3.6.5
• numpy 1.15.4
• pandas 0.23.4
• matplotlib 3.0.2
• seaborn 0.9.0
• scikit-learn 0.20.0