To jak klasyfikujemy kod zależy od ilości operacji, które muszą zostać wykonane przez kompter w celu otrzymania wyniku
Jak zmienia się czas potrzebny do wykonania operacji w zależności od ilości danych?
O(1)
function AddUpTo(n){
return n * (n+1) / 2;
}O(n)
function addUpTo(n){
let total = 0
for(let i = 1; i <= n; i++){
total +=1
}
return total
}O(n^2)
- Operacje arytmetyczne są constantami
- Przypisanie zmiennej to constant
- Dostęp do elementów array (za pomocą indeksu) albo obiektu (za pomocą klucza) jest constant
- Złożoność pętli zależy od długości pętli razy złożoność tego co dzieje się w środku pętli
Złożoność przestrzenna algorytmu to całkowita przestrzeń zajmowana przez algorytm w odniesieniu do rozmiaru danych wejściowych.
- Insertion, Removal, Access - O(1)
- Searching - O(n)
- Insertion, Removal - zalezy gdzie dodajemy, odejmujemy element. Jesli dodajemy nowy element do array za pomoca push, to taka operacja bedzie constant O(1). Jesli chcemy dodac nowy element na poczatku array, to array musi pozmieniac wszystkie indexy itd, ma wiecej operacji do wykonania O(n).
- Searching - O(n)
- Access - O(1)
Metody:
- push, pop - O(1)
- shift, unshift, concat, slice, splice - O(n)
- sort - O(n*logn)
- forEach, map, filter,
Zanim zaczniesz pisać kod, weź krok wstecz i postaraj się zrozumieć zadanie, które masz wykonać. Dokładne zbadanie problemu, pytania bardzo ułatwia wyjaśnienie rzeczy.
- Czy potrafię sparafrazować problem w swoich własnych słowach?
- Jakie inputy wchodzą do problemu
- Jakie outputy powinny wyjśc z problemu?
- Czy mam wystarczająco dużo informacji żeby rozwiązac problem?
- Jak powinienem nazwać ważne elementy danych, które są częścią problemu?
Wymyślanie konkretnych przykładów pozwala ci na lepsze zrozumienie problemu.
- Zacznij z prostymi przykładami
- Pomyśl o bardziej złożonych przykładach
- Pomyśl o przykładach z pustymi inputami i invalid inputami
Rozbij na mniejsze kroki, dobre tutaj są komentarze z krokami, które trzeba podjąć. Rozpisz najbardziej podstawowe kroki zanim zaczniesz pisac kod, to zmusza cię do myslenia nad kodem zanim zaczniesz go pisać.
- Jeśli nie potrafisz rozwiązac problemu, spróbuj tymczasowo zignorować część problemu, która sprawia ci trudność.
- Stwórz uproszczone rozwiązanie problemu i włącz do tego rozwiązania część, która ci sprawiała trudność
Napisanie działającego kodu to nie koniec.
Spójrz na indywidualne komponenty linijka po linijce i omów te części kodu, które ci się nie podobają. Kod potrzebuje balansu między wydajnością i czytelność
przykład kodu O(n), zastosowanie trzech oddzielnych pętli jest tutaj ok i jest to lepsze rozwiązanie od stosowania nested pętli, które dałyby O(n^2)
function validAnagram(a,b){
if(a.length !== b.length){
return false
}
let counter1 = {}
let counter2 = {}
for(let word of a){
counter1[word] = (counter1[word] ? counter1[word]+=1: counter1[word] = 1)
}
for(let word of b){
counter2[word] = (counter2[word] ? counter2[word]+=1: counter2[word] = 1)
}
for(let key in counter1){
if(!(key in counter2)){
return false
}
}
return true
}
console.log(validAnagram("anagram", "nagaram"))Tworzenie wskaźników, które odpowiadają indeksowi lub pozycji i przesuwają się w kierunku początku, końca lub środka na podstawie określonego warunku
function sumZero(arr){
let left = 0
let right = arr.length - 1
while(left<right){
let sum = arr[left] + arr[right]
if(sum===0){
return [arr[left], arr[right]]
}else if(sum > 0){
right--
}else{
left++
}
}
}
sumZero([-4,-3,-2,-1,0,1,2,3,10]) // [-3,3]function countUniqueValues(arr){
if(arr.length === 0) return 0
let i = 0
for(let j = 1; j < arr.length; j++){
if(arr[i] !== arr[j]){
i++
arr[i] = arr[j]
}
}
return i+1
}
countUniqueValues([1,1,1,2,3,3,4,5,6])Przydaje się kiedy działamy na array i szukamy jakiegos podzbioru tego array, który jest w jakiś sposób ciągły
function maxSubarraySum(arr, number){
let maxSum = 0
let tempSum = 0
if(arr.length < number) return null
for(let i = 0; i < number; i++){
tempSum += arr[i]
}
maxSum = tempSum
for(let i = number; i < arr.length; i++){
tempSum = tempSum - arr[i-number] + arr[i]
maxSum = Math.max(tempSum, maxSum)
}
console.log(maxSum)
}
maxSubarraySum([2,6,9,2,1,8,5,6,3], 3)Rozdzielanie danych na mniejsze kawałki i powtarzanie procesu z podzbiorem, subsetem tych danych
- A process that calls itself.
Recursive funkcje dodają ciągle nowe funkcje do call stack
Base Case - moment w którym recursive funkcja kończy się
Różny input - za każdym razem kiedy wywołujemy funkcje chcemy zeby miala inny input niz wczesniej
function sumRange(num){
if(num === 1) return 1;
return num + sumRange(num-1)
}
sumRange(3) // => 6=> sumRange(3)
return 3 + sumRange(2)
return 2 + sumRange(1)
return 1dla num = 3 funkcja zwraca 3 + sumRange(2)
funkcja jest powtarzana az do spotkania z Base Case
3 + sumRange(2) czeka na sumRange(2), ktore czeka na 2 + sumRange(1)
function silnia(num){
if(num === 1) return 1
return num * silnia(num-1)
}
silnia(5) // => 120function outer(input){
let outerScopedVariable = []
function helper(helperInput){
// modify the outerScopeVariable
helper(helperInput--)
}
helper(input)
return outerScoperVariable
}function collectOddValues(arr){
let result = []
function helper(helperInput){
if(helperInput.length === 0){
return
}
if(helperInput[0] % 2 !== 0){
result.push(helperInput[0])
}
helper(helperInput.slice(1))
}
helper(arr)
return result
}function collectOddValues(arr){
let newArr = [];
if(arr.length == 0){
return newArr
}
if(arr[0] % 2 !== 0){
newArr.push(arr[0])
}
newArr = newArr.concat(collectOddValues(arr.slice(1)))
return newArr
}
collectOddValues([1,2,3,4,5]) // => [1,3,5]collectOddValues([1,2,3,4,5]) // => [1,3,5]
[1].concat(collectOddValues([2,3,4,5]))
[].concat(collectOddValues[3,4,5])
[3].concat(collectOddValues[4,5])
[].concat(collectOddValues[5])
[5].concat(collectOddValues[])
[]indexOf , includes , find i findIndex - wszystkie te metody to linear search.
Po kolei sprawdzają każdy item dopóki nie znajdą pasującego elementu. Linear search jest O(n) chyba, ze element jest na poczatku arraya wtedy znajdujemy szybko. Im dluzszy array tym dluzszy średni czas szukania elementu.
Binary search jest duzo szybszy, zamiast eliminowania jednego elementu na raz (linear search sprawdza jeden, eliminuje i idzie do nastepnego) mozna wyeliminowac polowe elementow na raz. Binary search dziala tylko na posortowanych arrayach! Sredni czas to O(logn)
Szukamy połowe posortowanego arraya i sprawdzamy czy wybrany środek jest przed czy po elemencie, którego szukamy. Z połowy wybieramy następną połowe itd.
const sortedNumbers = [2, 5, 8, 11, 15, 23, 37, 42, 56, 68];
function binarySearch(array, value){
// tworzymy trzy wskazniki
let left = 0
let right = array.length-1
let middle = Math.round((left+right)/2)
while(array[middle] !== value && left <= right){
// left musi byc mniejszy/rowny right bo inaczej funkcja bedzie trwala w nieskonczonosc
// przesuwamy wskazniki w zaleznosci od tego czy middle jest mniejszy czy wiekszy
if(array[middle] > value) right = middle-1
else left = middle+1
middle = Math.round((left+right)/2)
}
if(array[middle] === value) return middle
else return -1
}
console.log(binarySearch(sortedNumbers,37))Sortowanie jest bardzo często używane w programowaniu, dobrze jest zrozumieć jak działa algorytm sortowania a każdy algorytm ma swoje wady i zalety
Javascript ma metodę array.sort() , domyślna kolejność sortowania wg. unicode. Przy domyślnych ustawieniach metoda jest przydatna tylko przy stringach, na numerach nie dziala. Można stworzyć funkcje porównującą, która bierze dwie wartości a i b , jeśli funkcja zwraca wynik ujemny to a jest przed b, dla wyniku dodatniego b jest przed a, dla zera są w tym samym miejscu
Bubble sort porównuje dwie wartości, jeśli jedna jest większa od drugiej to swapujemy, zamieniamy je miejscami. Funkcja kilka razy będzie przemielała funkcję w taki sposób, że największe wartości bąbelkują na górę (na koniec).
Ten algorytm nie jest często używany, ale jest dobrym problemem.
function bubbleSort(array){
let noSwaps // ta zmienna bedzie sprawdzac czy podczas loopa zrobilismy swapa
for(let i = array.length; i > 0; i--){
console.log(array)
let noSwaps = true // domyslnie jest true, jesli zrobimy swapa bedzie false
// idziemy od tylu zeby zmniejszac liczbe odpalania sie petli za
// kazdym razem kiedy znaleziona liczba wybąbelkuje na góre.
// Dlatego j < i-1
for(let j = 0; j<i-1; j++){
if(array[j] > array[j+1]){
swap(array, j,j+1)
noSwaps = false
}
}
// jesli nie zrobilismy swapa to znaczy, ze array jest juz posortowany
// nie ma sensu ciągle go mielić aż do końca pętli bo nie wprowadzamy
// już żadnych zmian, dlatego przerywamy pętle i zwracamy wynik
if(noSwaps)break
}
return array
}Funkcja swap
function swap(array, index1, index2){
let temp = array[index1]
array[index1] = array[index2]
array[index2] = temp
// es2015
// [array[index1], array[index2]] = [array[index2], array[index1]]
}Podobny do bubble sort tylko zamiast ukladac najpierw najwyższe wartości to wstawia najmniejsze na początek.
Selection sort jest O(n^2)
function selectionSort(array){
for(let i = 0; i < array.length; i++){
let minIndex = i
for(let j = i+1; j < array.length; j++){
if(array[j] < array[minIndex]) minIndex = j
}
if(i !== minIndex) swap(array, i, minIndex)
}
return array
}Insertion sort stopniowo tworzy większą lewą porcję array, która jest zawsze posortowana. Algorytm zapamiętuję sub array i wstawia następne wartości między te już posortowane. Insertion sort jest przydatny kiedy mamy do czynienia z wpływającymi danymi i od razu chcemy je sortować.
Insertion sort jest O(n^2)
function insertionSort(array){
for(let i = 1; i < array.length; i++){
let currentValue = array[i]
let j
// inner loop zaczyna sie na indeksie o 1 mniejszym od i
// leci w dół porównując wartości
// && array[h] > currentValue zapobiega tutaj niepotrzebnemu loopowaniu
// i porównywaniu wartości, które i tak są mniejsze po co więc je porównywać
// ten conditional jest tez bramką bo zawsze sprawdza czy wartośc jest większa od currentValue
for(j = i-1; j >= 0 && array[j] > currentValue; j--){
array[j+1] = array[j] // jesli array[j] jest wieksze od array[j+1] to zmieniamy
}
array[j+1] = currentValue // tutaj podmieniamy
}
return array
}Merge sort i następne algorytmy są lepsze od poprzednich.
Merge sort rozdziela array na mniejsze arraye z pojedynczymi elementami. Algorytm porównuje pojedyncze elementy i sprawdza, który jest większy i tworzy arraye z dwoma elementami, następnie porównuje posortowane już arraye i tworzy następne itd. Wynikiem jest nowy posortowany array
Merge sort jest O(nlogn)
funkcja merge:
function merge(arr1, arr2) {
let result = [];
let i = 0;
let j = 0;
while (i < arr1.length && j < arr2.length) {
if (arr1[i] < arr2[j]) {
result.push(arr1[i]);
i++;
} else {
result.push(arr2[j]);
j++;
}
}
// jeżeli arr1 i arr2 nie mają takiej samej liczby elementów to po
// zakończeniu porównywania trzeba te elementy dodać do wyniku
// dwa while loopy poniżej dbają o to żeby pozostale
// wartości w arrayach zostały dodane do wyniku
while (i < arr1.length) {
result.push(arr1[i]);
i++;
}
while (j < arr2.length) {
result.push(arr2[j]);
j++;
}
return result;
}
console.log(merge([1, 10, 50], [2, 14, 99, 100]));mergeSort:
function mergeSort(arr) {
if (arr.length <= 1) return arr; // base case
let middle = Math.floor(arr.length / 2);
// niech mergeSort([61,30,21,14])
// 1. array przechodzi checka i idzie dalej
// 2. array jest podzielony na [61,30] i [21,14]
// 3. [61,30] wchodzi do recursive funkcji i jest rozdzielany na [61] i [30]
// w zależności od wielkości array callstack będzie się powiększać i
// poprzednia wartość będzie czekała na następną
// [61] wchodzi do recursive funkcji i zwraca [61]
// [30] wchodzi do recursive funkcji i zwraca [30]
// uruchamiamy merge i dostajemy [30, 61] - to jest wartość leftHalf
// 4. [21,14] wchodzi do recursive funkcji i jest rozdzielany tak jak wyżej
// (...)
// wartość rightHalf to [14,21]
// 5. odpalamy merge i dostajemy wynik [14,21,30,61]
let leftHalf = mergeSort(arr.slice(0, middle)); // recursive case
let rightHalf = mergeSort(arr.slice(middle)); // recursive case
return merge(leftHalf, rightHalf)
}
console.log(mergeSort([61, 30, 21, 14,]));obieramy jakiś pivot point, sprawdzamy ile jest mniejszych wartości od pivot wartości w array i wstawiamy je przed ten pivot point (nie muszą być w tym momencie posortowane), szukając tych wartości zapisujemy ile ich znaleziono, pivot point przeskakuje do przodu o tą wartość. Operujemy ciągle na jednym arrayu i czynności te są powtarzane rekursywnie.
Time complexity to O(nlogn)
pivot funkcja
function pivot(array, startIndex = 0, endIndex = array.length - 1) {
let pivot = array[startIndex];
let currentPivotIndex = startIndex;
for (let i = startIndex + 1; i <= endIndex; i++) {
if (array[i] < pivot) {
currentPivotIndex++;
swap(array, currentPivotIndex, i)
}
}
swap(array, startIndex, currentPivotIndex)
console.log(array);
return currentPivotIndex;
}
const unsortedNumbers = [4, 8, 2, 1, 5, 7, 6, 3];
console.log(pivot(unsortedNumbers));quick sort
function quickSort(arr, left = 0, right = arr.length - 1) {
// kiedy left i right są takie same oznacza to, że po
// rekursywnym odpalaniu funkcji quicksort doszliśmy do momentu
// w którym subarray ma jeden element
if (left < right) {
let pivotIndex = pivot(arr, left, right);
//left
quickSort(arr, left, pivotIndex - 1);
//right
quickSort(arr, pivotIndex + 1);
}
return arr;
}Wszystkie poprzednie sorty należą do algorytmów sortujących porównujących, najlepsze time complexity możliwe przy tych algorytmach to O(nlogn). Radix sort niczego nie porównuje, jest specjalny i działa na liczbach. Wykorzystuje informacje o wielkości cyfr - więcej cyfr to większa liczba.
Radix tworzy 9 bucketów i sprawdza pierwszą cyfre od prawej strony każdego elementu array i grupuje liczby według tej cyfry, tworzy to ten sam array ale inaczej uporządkowany. Potem powtarzamy operacje na nowym arrayu dla następnej cyfry.
Radix sort jest O(nk), gdzie n - długość array, k - średnia liczba cyfr
helper funkcje do radix sort
function getDigit(num,place){
return Math.floor(Math.abs(num)/Math.pow(10,place) % 10)
}
function digitCount(num){
if(num === 0) return 1
return Math.floor(Math.log10(Math.abs(num))) + 1
}
function mostDigits(arr){
let max = arr[0]
for(number of arr){
if(number > max) max = number
}
return digitCount(max)
}radixSort
function radixSort(arr){
const largestNumberOfDigits = mostDigits(arr)
for(let k = 0; k <= largestNumberOfDigits; k++){
let buckets = {0: [], 1:[], 2:[], 3:[], 4:[], 5:[], 6:[], 7:[], 8:[], 9:[]}
for(number of arr){
const digit = getDigit(number, k)
buckets[digit].push(number)
}
arr = [].concat(...Object.values(buckets));
}
return arr
}Data structures to kolekcje wartości, relacji między nimi i funkcje albo operacje, które mogą być zastosowane do danych. Tworzymy klasy i dodajemy do nich funkcjonalność
Klasa to blueprint do tworzenia obiektów z predefiniowanymi właściwościami i metodami
Klasa powinna zaczynać się od wielkiej litery
this odnosi się do instancji klasy, czyli nowego obiektu stworzonego przez tą klasę
class Student {
constructor(firstName, lastName) {
this.firstName = firstName;
this.lastName = lastName;
}
}
let firstStudent = new Student("John", "Doe")
let secondStudent = new Student("Jan", "Kowalski")class Student {
constructor(firstName, lastName) {
this.firstName = firstName;
this.lastName = lastName;
this.scores = []
}
fullName() {
console.log(`Your full name is ${this.firstName} ${this.lastName}`);
}
addScore(score){
this.scores.push(score)
console.log(this.scores)
}
calculateAverage(){
const average = this.scores.reduce((a,b)=>a+b)/this.scores.length
console.log(average)
}
}
let firstStudent = new Student("John", "Doe");
firstStudent.fullName();
firstStudent.addScore(5)
firstStudent.addScore(2)
firstStudent.calculateAverage()static methody są uruchamiane bez tworzenia instancji ich klasy i nie mogą być uruchamiane przez instancje klasy. Są to utility functions
class Circle {
constructor(radius) {
this.radius = radius;
}
getArea() {
return Math.PI * this.radius * this.radius;
}
static compareCircles(circle1, circle2) {
console.log(circle1.getArea() > circle2.getArea() ? circle1 : circle2
}
}
const circle1 = new Circle(3);
const circle2 = new Circle(4);
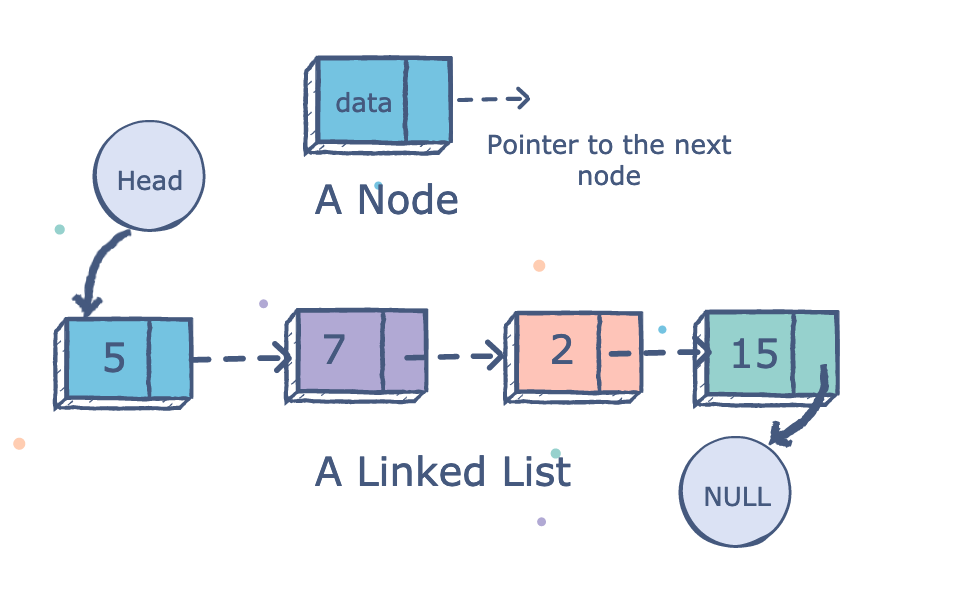
Circle.compareCircles(circle1, circle2);Linked list zawiera elementy bez indeksów, które wskazują na następny element. Linked lista złożona jest z node’ów, każdy node ma wartość i next pointer, który wskazuje na następny node albo null. Random access nie istnieje, trzeba przejśc przez każdy element. Skoro nie ma indeksów to nie ma problemu z dodawaniem wartości na początku, dodajemy po prostu nowy head, który wskazuje na stary head. W arrayach dodawanie elementu na początek sprawia, że trzeba przesuwać wszystkie indeksy. Singly linked lista to lista w której każdy node jest połączony tylko z jednym node’m, jednokierunkowo
// node zawiera val i next
// piece of data - val
// reference to the next node - next
class Node{
constructor(val){
this.val = val
this.next = null
}
}
let first = new Node(1)
first.next = new Node(2)
first.next.next = new Node(3)
// first => { val: 1, next: Node { val: 2, next: Node { val: 3, next: null } } }push
class SinglyLinkedList {
constructor() {
this.length = 0;
this.head = null;
this.tail = null;
}
push(val) {
const newNode = new Node(val);
if (!this.head) {
this.head = newNode;
this.tail = newNode;
} else {
this.tail.next = newNode;
this.tail = newNode;
}
this.length++;
return this;
}
}pop
pop() {
if (!this.head) return undefined;
if (this.length === 1) {
const poppedNode = this.head;
this.head = null;
this.tail = null;
return poppedNode.val;
}
//
let currentNode = this.head;
let previousNode = null;
while (currentNode.next) {
previousNode = currentNode;
currentNode = currentNode.next;
}
this.tail = previousNode;
this.tail.next = null;
this.length--;
if(this.length === 0)this.tail = null
return currentNode.val;
}shift
shift(){
const currentHeadNode = this.head
if(!(currentHeadNode)) return undefined
this.head = currentHeadNode.next
this.length--
return currentHeadNode.val
}unshift
unshift(val){
const currentHeadNode = this.head
const newHeadNode = new Node(val)
newHeadNode.next = currentHeadNode
this.head = newHeadNode
if(!currentHeadNode) this.tail = newHeadNode
this.length++
return this
}set
set(index, value){
const foundNode = this.get(index)
if(!foundNode) return false
foundNode.val = value
return true
}insert wykorzystuje poprzednie metody
insert(index, value) {
if (index > this.length || index < 0) return false;
if (index === this.length) return !!this.push(value);
if (index === 0) return !!this.unshift(value);
let targetNode = this.get(index);
let previousNode = this.get(index - 1);
let newNode = new Node(value);
newNode.next = targetNode;
previousNode.next = newNode;
this.length++;
return true;
}remove
remove(index){
if(index < 0 || index > this.length-1) return undefined
if(index === this.length-1) return !!this.pop()
if(index === 0 ) return !!list.shift()
let targetNode = this.get(index)
let previousNode = this.get(index-1)
previousNode.next = targetNode.next
this.length--
return previousNode
}reverse
reverse() {
let initialHead = this.head;
let initialTail = this.tail;
this.head = initialTail;
this.tail = initialHead;
let nextNode;
let currentNode = initialHead;
let prevNode = null;
for (let i = 0; i < this.length; i++) {
nextNode = currentNode.next;
currentNode.next = prevNode;
prevNode = currentNode;
currentNode = nextNode;
}
return this
}insertion - O(1)
removal - O(1) albo O(n) , zalezy skąd usuwamy
searching - O(n)
access - O(n)
Singly linked listy są dobrą alternatywą dla arrayów, kiedy wstawianie i usuwanie na początku są często używane
Prawie to samo co singly linked lists, różnica jest taka, że każdy node ma pointer wskazujący na poprzedniego node’a. Każdy node wskazuje na następny i poprzedni node.
class Node{
constructor(val, next, prev){
this.val = val
this.next = null
this.prev = null
}
}
class DoublyLinkedList{
constructor(head,tail,length){
this.head = null
this.tail = null
this.length = 0
}
} push(val) {
const newNode = new Node(val);
if (this.length === 0) {
this.head = newNode;
this.tail = newNode;
} else {
this.tail.next = newNode
newNode.prev = this.tail
this.tail = newNode;
}
this.length++;
return this;
}pop() {
const currentTail = this.tail;
if (!this.head) return undefined;
if (this.length === 1) {
this.head = null;
this.tail = null;
} else {
this.tail = currentTail.prev;
this.tail.next = null;
}
this.length--;
return currentTail;
}shift() {
const oldHead = this.head;
if(this.length === 0) return undefined
if (this.length === 1) {
this.head = null;
this.tail = null;
} else {
this.head = oldHead.next;
this.head.prev = null;
oldHead.next = null
}
this.length--;
return oldHead;
} unshift(value) {
const newNode = new Node(value);
if (this.length === 0) {
this.head = newNode
this.tail = newNode
} else {
const oldHead = this.head;
oldHead.prev = newNode;
newNode.next = oldHead;
this.head = newNode;
}
this.length++;
return this
} get(index) {
if (index < 0 || index >= this.length) return null;
let count, current;
if (index <= this.length / 2) {
count = 0;
current = this.head;
while (count !== index) {
current = current.next;
count++;
}
return current;
} else {
count = this.length - 1;
current = this.tail;
while (count !== index) {
current = current.prev;
count--;
}
return current;
}
}insert(index, value){
if(index < 0 || index > this.length) return false
if(index === 0) return this.unshift(value)
if(index === this.length) return this.push(value)
const newNode = new Node(value)
const beforeNode = this.get(index-1)
const afterNode = beforeNode.next
beforeNode.next = newNode
newNode.prev = beforeNode
newNode.next = afterNode
afterNode.prev = newNode
this.length++
return true
} remove(index){
if(index < 0 || index > this.length) return undefined
if(index === 0) return this.shift()
if(index === this.length-1) return this.pop()
let targetNode = this.get(index)
let beforeNode = targetNode.prev
let afterNode = targetNode.next
beforeNode.next = afterNode
afterNode.prev = beforeNode
targetNode.prev = null
targetNode.next = null
this.length--
return targetNode
}insertion - O(1)
removal - O(1)
searching - O(n)
access - O(n)
Doubly linked listy są szybsze w szukaniu node’ów od singly, to jednak zabiera więcej pamięci
LIFO - Last In First Out
Stack to abstrakcyjna struktura danych
Ostatnia rzecz (na samej górze) jest usuwana jako pierwsza (np. stos talerzy)
Stack jest tylko koncepcją i nie ma jednej prawidłowej metody do tworzenie stacka. Łatwo jest stworzyć stack przy pomocy array, ale nie jest to najlepsze rozwiązanie bo nie używamy indeksów.
// Browser nav stack example
let stack1 = []
stack1.push("google")
stack1.push("youtube")
stack1.push("wikipedia")
stack1.pop()
console.log(stack1)
// Photoshop stack example
let stack2 = []
stack2.unshift("create")
stack2.unshift("resize")
stack2.unshift("copy")
stack2.shift()
console.log(stack2)
// push i pop jest lepszym rozwiązaniem bo nie trzeba reindeksować całego arrayMetody array nie są potrzebne w stacku, stack to tylko dodawanie i usuwanie według LIFO dlatego można zrobić stacka za pomocą singly linked list.
Tutaj używamy shift i unshift, ponieważ interesuje nas tylko dodawanie nowych elementów i usuwanie z początku stacka. W zwykłym singly linked list używałem push i pop, pop jest O(n) bo musi przeiterować przez każdy element a shift jest constant bo używa tylko pierwszego elementu.
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class Stack {
constructor() {
this.first = null;
this.last = null;
this.size = 0;
}
unshift(value) {
let newNode = new Node(value);
if (!this.first) {
this.first = newNode;
this.last = newNode;
} else {
let currentFirst = this.first;
newNode.next = currentFirst;
this.first = newNode;
}
this.size++;
}
shift() {
if (this.size === 0) return null;
const currentFirst = this.first;
if (this.size === 1) {
this.first = null;
this.last = null;
} else {
let afterFirst = this.first.next;
this.first = afterFirst;
this.size--;
}
return currentFirst.value;
}
}Stack priorytezuje insertion i removal, searching i access nie mają tutaj znaczenia
insertion - O(1)
removal - O(1)
searching - O(n)
access - O(n)
Tak jak w stackach, queue opiera się na dwóch operacjach - dodawaniu i usuwaniu danych
FIFO - First In First Out
Łatwe rozwiązanie używając array
let queue = []
queue.push("FIRST")
queue.push("SECOND")
queue.push("THIRD")
queue.shift()
console.log(queue)Tutaj używamy singly linked list i dwie metody - push i shift, które mają nazwę enqueue i dequeue
class Node {
constructor(value) {
this.value = value;
this.next = null;
}
}
class Queue {
constructor() {
this.first = null;
this.last = null;
this.size = 0;
}
enqueue(val) {
const newNode = new Node(val);
if (!this.first) {
this.first = newNode;
this.last = newNode;
} else {
let lastNode = this.last;
lastNode.next = newNode;
this.last = newNode;
}
this.size++;
}
dequeue() {
if (!this.first) return null;
let firstNode = this.first;
if (this.first === this.last) {
this.last === null;
} else {
let secondNode = this.first.next;
this.first = secondNode;
}
this.size--;
return firstNode.value;
}
}Tak samo jak Stacki znaczenie mają tutaj tylko insertion i removal. Są constant tylko w rozwiązaniu z singly linked lists, arraye nie mają tego samego Big O.
insertion - O(1)
removal - O(1)
searching - O(n)
access - O(n)
Tree to struktura danych, która składa się z node’ów w relacji parent / child.
Root to node na samej górze, istnieje tylko jeden root
Child nie może wskazywać na parent, node nie może wskazywać na sibling
Siblings to grupa node’ów z jednym parentem
Leaf to node bez children
Drzewka są nielinearne, listy były linearne.
Binary tree node może mieć maksymalnie dwa children
- Każdy parent node może mieć maksymalnie 2 children
- Children node z lewej strony parent node jest mniejszy od parent
- Children node z prawej strony parent node jest większy od parent
class Node{
constructor(value){
this.value = value
this.left = null
this.right = null
}
}
class BinarySearchTree{
constructor(){
this.root = null
}
}insert(value) {
const newNode = new Node(value);
if (this.root === null) {
this.root = newNode;
return this;
} else {
let currentNode = this.root;
// while loop bedzie dzialal dopoki nie znajdzie miejsca do wstawienia
while (true) {
// jesli trafimy na duplikat
if (value === currentNode.value) return undefined;
// LEFT
if (value < currentNode.value) {
// jesli nie ma po lewej node to wstawiamy go tam i git
if (currentNode.left === null) {
currentNode.left = newNode;
return this;
} else {
currentNode = currentNode.left;
}
}
// RIGHT
else if (value > currentNode.value) {
if (currentNode.right === null) {
currentNode.right = newNode;
return this;
} else {
currentNode = currentNode.right;
}
}
}
}
} find(value) {
if (this.root === null) return false;
let currentNode = this.root;
let found = false;
while (currentNode && !found) {
if (value < currentNode.value) {
currentNode = currentNode.left;
} else if (value > currentNode.value) {
currentNode = currentNode.right;
} else {
found = true;
}
}
if(!found) return undefined
return currentNode;
}Binary search tree są wydajne dlatego, że kiedy podwajamy ilość node’ów to liczba operacji insert/find wzrasta tylko o 1 step
insertion - O(logn)
searching - O(logn)
W jaki sposób odwiedzić każdego node’a?
- Breadth First Search (poziomo)
- Depth First Search (pionowo)
- DFS Preorder
- DFS Inorder
- DFS Postorder
BFS() {
let currentNode = this.root;
let queue = [];
let visited = [];
queue.push(currentNode);
while (queue.length > 0) {
currentNode = queue.shift();
if (currentNode.left) queue.push(currentNode.left);
if (currentNode.right) queue.push(currentNode.right);
visited.push(currentNode.value);
}
return visited;
} DFSPreorder() {
let currentNode = this.root;
let visited = [];
function traverse(node) {
visited.push(node.value);
if (node.left) traverse(node.left);
if (node.right) traverse(node.right);
}
traverse(currentNode);
return visited;
} DFSPostorder() {
let currentNode = this.root;
let visited = [];
function traverse(node) {
if (node.left) traverse(node.left);
if (node.right) traverse(node.right);
visited.push(node.value);
}
traverse(currentNode);
return visited;
} DFSInorder() {
let currentNode = this.root;
let visited = [];
function traverse(node) {
if (node.left) traverse(node.left);
visited.push(node.value);
if (node.right) traverse(node.right);
}
traverse(currentNode);
return visited;
}Przy większych, szerszych drzewkach lepiej jest używać DFS, ponieważ zajmujemy się jednym branchem na raz. BFS ciągle dodaje i usuwa elementy z kolejki, space complexity jest większe.
Binary heap jest podobne do binary tree, ale ma inne zasady
Używane w priority queues i graph traversal
- MaxBinaryHeap - parent node’y są zawsze większe od child node’ów
- MinBinaryHeap - parent node’y są zawsze mniejsze od child node’ów
Każdy parent może mieć max 2 children
Nie ma podziału na mniejsze po lewej i większe po prawej tak jak w binary tree
Binary Heap można zapisać w array
Dla parent node o indeksie n lewy child tego elementu znajduje się na indeksie 2n+1 a prawy na indeksie 2n+2
Możemy też znaleźć indeks parenta na podstawie indeksu child, dla każdego child node o indeksie n jego parent jest na indeksie Math.floor((n-1)/2)
class MaxBinaryHeap {
constructor() {
this.values = [41, 39, 33, 18, 27, 12];
}
insert(value) {
this.values.push(value);
this.bubbleUp();
}
bubbleUp() {
let index = this.values.length - 1;
const element = this.values[index];
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.values[parentIndex];
if (element <= parent) break;
// swap
this.values[parentIndex] = element;
this.values[index] = parent;
index = parentIndex;
}
}
}extractMax() {
const max = this.values[0];
let lastValue = this.values[this.values.length - 1];
if(this.values.length > 0){
this.values[0] = lastValue;
this.values.pop();
this.bubbleDown();
return max;
}
}
bubbleDown() {
const value = this.values[0];
const length = this.values.length;
let currentIndex = 0;
while (true) {
let leftChildIndex = 2 * currentIndex + 1;
let rightChildIndex = 2 * currentIndex + 2;
let leftChild;
let rightChild;
// swapIndex za kazdym loopem jest null i zmieniamy jego wartosc
// wtedy kiedy znajdziemy wiekszego child
let swapIndex = null;
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex];
if (leftChild > value) {
swapIndex = leftChildIndex;
}
}
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex];
if (
(swapIndex === null && rightChild > value) ||
(swapIndex !== null && rightChild > leftChild)
) {
swapIndex = rightChildIndex;
}
}
// jesli nie ma swapIndex to znaczy, ze nie znalezlismy
// zadnego childa do zmiany czyli koniec
if (swapIndex === null) break;
// swap
this.values[currentIndex] = this.values[swapIndex];
this.values[swapIndex] = value;
currentIndex = swapIndex;
}
}Każdy element priority queue ma priority, elementy z wyższym priorytetem wychodzą z kolejki wcześniej niż elementy z niższym priorytetem
Ponizszy kod jest prawie taki sam jak jak wyzej z tym, ze tutaj stosujemy MinBinaryHeap i dzialamy na node’ach z wartosciami value i priority
class Node {
constructor(value, priority) {
this.value = value;
this.priority = priority;
}
}
class PriorityQueue {
constructor() {
this.values = [];
}
enqueue(value, priority) {
const newNode = new Node(value, priority);
this.values.push(newNode);
this.bubbleUp();
}
bubbleUp() {
let index = this.values.length - 1;
const element = this.values[index];
while (index > 0) {
let parentIndex = Math.floor((index - 1) / 2);
let parent = this.values[parentIndex];
if (element.priority >= parent.priority) break;
this.values[parentIndex] = element;
this.values[index] = parent;
index = parentIndex;
}
}
dequeue() {
const min = this.values[0];
let lastNode = this.values[this.values.length - 1];
if (this.values.length > 0) {
this.values[0] = lastNode;
this.values.pop();
this.bubbleDown();
return min;
}
}
bubbleDown() {
const currentNode = this.values[0];
const length = this.values.length;
let currentIndex = 0;
while (true) {
let leftChildIndex = 2 * currentIndex + 1;
let rightChildIndex = 2 * currentIndex + 2;
let leftChild;
let rightChild;
let swapIndex = null;
if (leftChildIndex < length) {
leftChild = this.values[leftChildIndex];
if (leftChild.priority < currentNode.priority) {
swapIndex = leftChildIndex;
}
}
if (rightChildIndex < length) {
rightChild = this.values[rightChildIndex];
if (
(swapIndex === null && rightChild.priority < currentNode.priority) ||
(swapIndex !== null && rightChild.priority < leftChild.priority)
) {
swapIndex = rightChildIndex;
}
}
if (swapIndex === null) break;
// swap
this.values[currentIndex] = this.values[swapIndex];
this.values[swapIndex] = currentNode;
currentIndex = swapIndex;
}
}
}np. dla 16 elementów robimy 4 porównania
insertion - O(logn)
removal - O(logn)
search - O(n)
Hast Tables są używane do przechowywania key-value pairs
Żeby dostać się do wartości przy użyciu klucza trzeba przekonwertować klucze w prawidłowe oznaczenia array. Funkcja, która to robi nazywa się hash function.
Poniższa funkcja ma pare problemów - hashuje tylko stringi, nie jest constant time i może być losowa
function simpleHash(key, arrayLen){
let total = 0
for(let char of key){
let value = char.charCodeAt(0) - 96
total = (total + value) % arrayLen
}
return total
}Liczby pierwsze są czesto używane w hash funkcjach, zmniejszają prawdopodobieństwo kolizji
function hash(key, arrayLen){
let total = 0
let WEIRD_PRIME = 31
for(let i = 0; i < Math.min(key.length, 100); i++){
let char = key[i]
let value = char.charCodeAt(0) - 96
total = (total * WEIRD_PRIME + value) % arrayLen
}
return total
}Separate chaining polega na przechowywaniu danych w tym samym miejscu używając nested struktury danych (np. array albo linked list)
Tutaj zapisujemy tylko jeden kawałek danych na każdej pozycji a w przypadku kolizji szukamy następnego wolnego miejsca
class HashTable {
// chcemy zeby size byl liczba pierwsza
constructor(size = 17) {
this.keyMap = new Array(size);
}
_hash(key) {
let total = 0;
let WEIRD_PRIME = 31;
for (let i = 0; i < Math.min(key.length, 100); i++) {
let char = key[i];
let value = char.charCodeAt(0) - 96;
total = (total * WEIRD_PRIME + value) % this.keyMap.length;
}
return total;
}
set(key, value) {
let index = this._hash(key);
// uzywamy separate chaining, jesli funkcja hash zwraca
// drugi raz ten sam indeks to na miejscu tego indeksu
// bedzie array, ktory ma w srodku dwa arraye key value
if (!this.keyMap[index]) {
this.keyMap[index] = [];
}
this.keyMap[index].push([key, value]);
return index;
}
get(key) {
let index = this._hash(key);
if (this.keyMap[index]) {
// ten loop jest po to zeby dostac prawidlowa value
// w sytuacji kiedy mamy wiecej niz jedna key value pair
// na indeksie, ktory dostajemy z hash function
for (let i = 0; i < this.keyMap[index].length; i++) {
if (this.keyMap[index][i][0] === key) {
return this.keyMap[index][i][1];
}
}
}
return undefined;
}
keys() {
let keys = [];
for (let i = 0; i < this.keyMap.length; i++) {
if (this.keyMap[i]) {
for (let j = 0; j < this.keyMap[i].length; j++) {
if (!keys.includes(this.keyMap[i][j][0]))
keys.push(this.keyMap[i][j][0]);
}
}
}
return keys;
}
values() {
let values = [];
for (let i = 0; i < this.keyMap.length; i++) {
if (this.keyMap[i]) {
for (let j = 0; j < this.keyMap[i].length; j++) {
if (!values.includes(this.keyMap[i][j][1]))
values.push(this.keyMap[i][j][1]);
}
}
}
return values;
}
}Dobra hash funkcja, która równomiernie rozdziela wszystkie wartości jest constant
insertion - O(1)
deletion - O(1)
access - O(1)
Graph to kolekcja node’ów i połączeń między tymi node’ami
Vertex - to node
Edge - połączenie między node’ami
Zastosowania:
- w portalach społecznościowych, za pomocą grafów można zapisać relacje między użytkownikami, znajomymi.
- mapy google
- recommendations engines
Graph może być undirected i directed
Graph może być weighted i unweighted
Tworzymy dwuwymiarową macierz sąsiedztwa w której zapisujemy relację między node’ami
Jeśli chcemy sprawdzić w jakiej relacji jest trójka z innymi node’ami to sprawdzamy wartość indeksu 3 arraya w którym jest nested array, czyli [1,2,5] to liczby w relacji z 3
Jeśli wartości nie są numearmi to możemy zapisać listę w postaci słownika np. D: [1, 2, 5]
Lista sąsiedztwa
- może zajmować mniej miejsca
- szybsze przechodzenie przez wszystkie edges
- może być wolniejsza przy wyszukiwaniu konkretnego edge’a
Macierz sąsiedztwa
- zajmuje więcej miejsca
- wolniejsze przechodzenie przez wszystkie edges
- szybsze wyszukiwanie konkretnego edge’a
class Graph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if (!this.adjacencyList[vertex]) {
this.adjacencyList[vertex] = [];
}
}
addEdge(vertex1, vertex2) {
this.adjacencyList[vertex1].push(vertex2);
this.adjacencyList[vertex2].push(vertex1);
}
removeEdge(vertex1, vertex2) {
this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
(v) => v !== vertex2
);
this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
(v) => v !== vertex1
);
}
removeVertex(vertex) {
while (this.adjacencyList[vertex].length) {
let adjacentVertex = this.adjacencyList[vertex].pop();
this.removeEdge(vertex, adjacentVertex);
}
delete this.adjacencyList[vertex];
}
} DFSRecursive(startVertex) {
let result = [];
let visited = {};
const adjacencyList = this.adjacencyList;
DFS(startVertex);
function DFS(vertex) {
if (!vertex) return null;
result.push(vertex);
visited[vertex] = true;
for (let neighbor of adjacencyList[vertex]) {
if (!visited[neighbor]) {
return DFS(neighbor);
}
}
}
return result;
} DFSIterative(startVertex) {
let stack = [];
let result = [];
let visited = {};
let currentVertex;
stack.push(startVertex);
while (stack.length > 0) {
currentVertex = stack.pop();
if (!visited[currentVertex]) {
visited[currentVertex] = true;
result.push(currentVertex);
for (let neighbor of this.adjacencyList[currentVertex]) {
if (!visited[neighbor]) {
stack.push(neighbor);
}
}
}
}
return result;
} BFS(startVertex) {
let queue = [startVertex];
let result = [];
let visited = {};
let currentVertex;
while (queue.length > 0) {
currentVertex = queue.shift();
result.push(currentVertex);
visited[currentVertex] = true;
for (let neighbor of this.adjacencyList[currentVertex]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
queue.push(neighbor);
}
}
}
return result;
}Algorytm Dijkstry znajduje najkrótszą drogę między dwoma vertexami na grafie.
Dijkstra wykorzstuje weighted graphy i priority queue (kolejka taka jak w binary heaps)
class WeightedGraph {
constructor() {
this.adjacencyList = {};
}
addVertex(vertex) {
if (!this.adjacencyList[vertex]) this.adjacencyList[vertex] = [];
}
addEdge(vertex1, vertex2, weight) {
this.adjacencyList[vertex1].push({ node: vertex2, weight });
this.adjacencyList[vertex2].push({ node: vertex1, weight });
}
}Dijkstra(startVertex, endVertex) {
let queue = new PriorityQueue();
let distances = {};
let previous = {};
let path = []
let smallest;
// initial state
for (let vertex in this.adjacencyList) {
if (vertex === startVertex) {
distances[vertex] = 0;
queue.enqueue(vertex, 0);
} else {
distances[vertex] = Infinity;
queue.enqueue(vertex, Infinity);
}
previous[vertex] = null;
}
while (queue.values.length > 0) {
smallest = queue.dequeue().val;
if (smallest === endVertex) {
while(previous[smallest]){
path.push(smallest)
smallest = previous[smallest]
}
break
}
if (smallest || distances[smallest] !== Infinity) {
for (let neighbor in this.adjacencyList[smallest]) {
// znajdz sasiada
let nextNode = this.adjacencyList[smallest][neighbor];
// oblicz nowy dystans do sasiada
let candidate = distances[smallest] + nextNode.weight;
let nextNeighbor = nextNode.node;
if (candidate < distances[nextNeighbor]) {
// aktualizacja nowego najmniejszego dystansu do sasiada
distances[nextNeighbor] = candidate;
// aktualizacja poprzedniego - w jaki sposob dostalismy sie do sasiada
previous[nextNeighbor] = smallest;
// enqueue z nowym priorytetem
queue.enqueue(nextNeighbor, candidate);
}
}
}
}
return path.concat(smallest).reverse()
}