'Cross'는 '상호'라는 의미를 가지고 있고 'Entropy'는 '무질서도(정확하게는 물질의 상태 변화)'라는 뜻입니다. '상호 관계'라는 말에는 적어도 둘 이상의 주체가 존재함을 내포하고 있습니다. 통계학적으로 쓰이는 Cross Entropy에서, Cross는 확률분포 p와 q라는 2개의 주체가 있고 그것들을 곱함을 의미합니다. 여기서 p와 q는 각각 실제 확률, 예측 확률입니다. Entropy는 어떤 확률변수가 나타낼 수 있는 상태의 총합으로 나타낼 수 있습니다. 즉, Cross Entorpy는 실제 확률과 예측 확률을 곱하고 더하는 수식으로 표현할 수 있습니다. Cross Entropy는 딥러닝에서 코스트 함수로 사용되는데, 로지스틱 회귀 코스트 함수를 통해 Cross Entropy를 이해해 보겠습니다. 아래는 로지스틱 회귀 코스트 함수입니다.

이렇게 되고, 이것이 Cross Entropy 수식입니다.
이전에 우리는 신경망의 코스트 함수로 'Mean Squared Error(MSE)' 방법을 썼습니다. 이 코스트 함수의 결과 값은 하나의 스칼라 값으로 나옵니다. 그러나 만약 신경망에 softmax 함수를 썼을 때, 그 결과로 나오는 output은 벡터 형태입니다. 하나의 벡터는 여러 output units 중 하나의 unit이 됩니다. 또한, label을 'one-hot coding'이라는 방법으로 벡터로 표현할 수 있습니다. 그 말은 즉, 자신의 number of class에 따라 벡터의 길이가 결정됩니다. 자신의 label은 1로 표시되고 나머지는 0으로 표시됩니다.
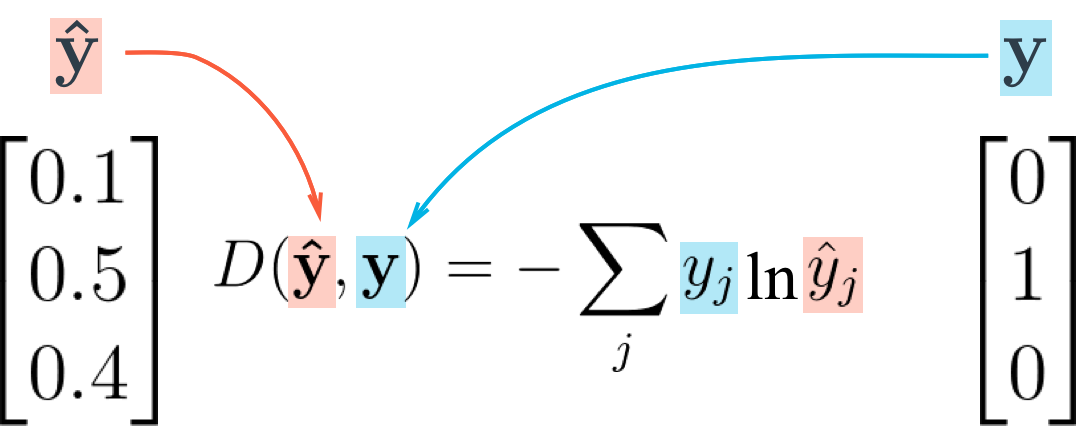
예를 들면, 0~9 까지의 수로 분류할 때 벡터의 길이는 10이 되고, '4' 레이블을 표현한다면 y(p) = [0,0,0,0,1,0,0,0,0,0]로 표현할 수 있습니다. ŷ(q) = [0.047,0.048,0.061,0.07,0.330,0.062,0.001,0.213,0.013,0.150] 이런식으로 표현될 것입니다. p와 q의 차이를 계산하기 위해 Cross Entropy를 사용합니다.
y가 label이고, ŷ가 prediction 값 입니다.
label(L)값이 [0,1]이라고 했을 때, prediction(ŷ) 값이 맞은 경우와 틀린 경우의 cost를 아래 예시를 통해 살펴보겠습니다. 아래 예시의 prediction 값은 극단적인 표현으로 [0,1] , [1,0]으로 표현했습니다. [0.2,0.8] 혹은 [0.6,0.4]등이 될 수도 있겠죠.
L은 label, S는 sigmoid 함수(activation function)를 거치고 나온 값(즉, 신경망을 거치고 나온 output) 입니다.
p*(-log(q))를 했을 때 cost 함수는 label값에 맞게 잘 예측 할 수록 0에 가깝고 틀릴 수록 ∞ 에 가까워집니다.
여기서 one-hot coding의 장점을 알 수 있습니다. 정답이 아닌 부분은 모두 0이기 때문에 신경망을 거치고 나온 output(prediction)과 곱해졌을 때 모두 0으로 처리됩니다. 결국, label에서 정답인 부분(1)에서의 prediction 값(어떠한 확률 값)만 코스트 함수의 연산을 거쳐 cost 값이 나옵니다.
텐서플로우를 이용한 코드 예제
import tensorflow as tf
cross_entropy = -tf.reduce_sum(y_*tf.log(y))
# y_ : label
# y : prediction