Geometry Easy
In the diagram below, $ABCD$ is a rectangle with side lengths $AB=3$ and $BC=11$, and $AECF$ is a rectangle with side lengths $AF=7$ and $FC=9,$ as shown. The area of the shaded region common to the interiors of both rectangles is $\frac mn$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.
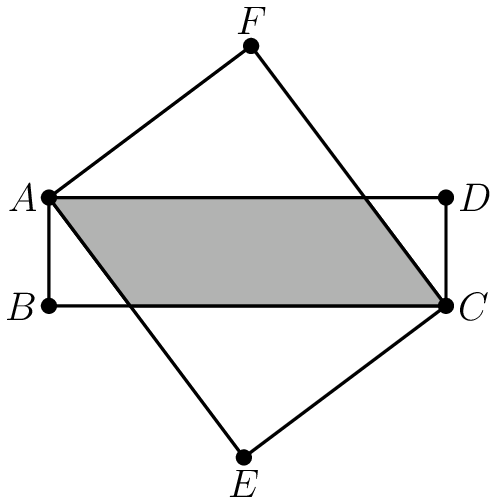
$AE$와 $BC$의 교점을 $P$라 두면 $\triangle ABP \sim \triangle CEP$
$CP$를 $x$라 두면 $BP=11-x$, $\triangle ABP : \triangle CEP = 3 : 7$이므로
$\frac73 (11-x) + \frac37 x = AE = 9$, 즉 $x = \frac{35}{4}, Area = \frac{105}{4}$
$\therefore Ans=109$