Ultrasonic SHM UGW Signal Analysis - Composite Material Delamination Detection

1. Introduction
2. Ultrasonic SHM
3. Problem definition
4. Selection of interpolation method
5. Library implementation
6. Use of the library
7. Analysis of used methods
8. Identification of delamination
9. Conclusion
10. References

The aim of this work was to develop an efficient algorithm for evaluation mutual shift of signals obtained during ultrasonic SHM by UGW method. Principle The method used is based on the identification of local maxima, their interpolation by a suitable course and finding the global maximum of this course. For interpolation 3 different techniques (PLI, CSI and ECI) were chosen for maxima. The signals shift subsequently used to detect delamination of the tested composite material. The result is distributed in the form of a C language library designed to meet general PPE paradigm. Input and output data are in CSV format, which is used in subsequent analysis in the MATLAB environment. The library was successfully tested on the system Linux.

1. Introduction

Damage detection and especially prevention is an important part of most industries industry, where, for example in aviation or aerospace, it is necessary and key element. Modern SHM methods using the principles of NDT (non - destructive testing) testing) have recently become increasingly emphasized in both scientific and environment and in practice.

Non-destructive testing aims to estimate residual life or risk associated with the use of a particular thing. In other words, using non-invasive techniques discover hidden defects that could only be detected by standard methods (partial) destruction of the thing. The history of NDT dates mostly to 1895, when X-rays were discovered, and thus began a new era of looking at objects without them damage. Today, it is commonly diagnosed non-destructively with, for example, electromagnetic, acoustic, optical, radiographic or thermal methods.

The general quality of the test is enhanced by an appropriate combination of these techniques, however, that as the complexity grows, so does the difficulty, and therefore the required expertise qualifications and know-how. This is especially true for NDT, because it almost always does it is not a simple and straightforward solution. When designing such a system is first it is necessary to analyze the situation, select a group of tested physical principles, develop a test method and build a measuring chain. In the next steps, the data measured and subsequently evaluated.

However, there is no guarantee that the data must be relevant or meaningful the result will be quite conclusive. Because sometimes looking for clues that prove It is necessary to proceed very much before changing the material before it occurs carefully and with some foresight and experience. It follows that NDT can be very time-consuming, financially and personally demanding. On the other hand, you can predict critical system failures and thus save costs or even save human lives.

2. Ultrasonic SHM

Ultrasonic non-destructive testing uses higher sound waves frequencies than what can be heard by humans, from about 20 kHz to tens to hundreds of MHz. This ripple is transmitted to the test material by which it partially it passes through and partially bounces off it. There are various methods, such as UT (Ultrasonic Testing) or UGW (Ultrasonic Guide Wave testing).

In the UT method, the test string usually consists of a signal generator, transmitter, receiver and signal analyzer. The generator and analyzer are classically formed by one device, which is visually similar to an oscilloscope. The transmitter and receiver can be used combined or dual, most commonly used today uses the piezoelectric effect for these purposes. The silicon membrane converts electrical energy to mechanical, and thus serves as a key element for transmission and acoustic signal reception. The principle is to send a wave to the test material and in the measurement of reflections. If there is a crack inside the homogeneous object, will appear on the screen as peak between two peaks, which indicates a reflection from surface, respectively from the bottom of the object.

The UGW method is most often used for pipeline inspection or detection delamination of objects. It is based on the propagation of a longitudinal (Lamb) wave through a surface (or just below the surface) of the test material from one point to another. See by changing the thickness of the material, the speed of propagation of the ultrasonic wave also changes. Thanks to it is possible to find even a slight one by comparing the reference and the tested signal structural defect.

3. Problem definition

We obtained data from measurements using the UGW method. These are digital samples ultrasonic waves that penetrated the surface of the tested composite object from point A to point B. Several waves were measured. The first is reference and corresponds signal without any structural defects. Additional waves were tested on materials with a certain degree of delamination. The aim is to correctly identify and possibly determining the degree of this delamination.

At first, the naked eye cannot say anything about this data. It is necessary to compare the measured waves with reference. The solution to this problem is to find the global envelope maximum signals. By subtracting the global maxima of the measured wave envelopes from the global maximum reference we get the shift of a specific signal. We move the whole by this value wave and plot it together with the reference wave. It is now clear that if a defect has occurred. If the wave was copying the reference, it was moving the same speed and the material should be free of defects. Otherwise, it probably happened to change the thickness of the material. The degree of delamination can then be determined, if known wave propagation speeds in both materials.

The signal envelope can be obtained in various ways. Among the most used are low-pass filtering, Hilbert transform, correlation, or interpolation local maxima by a suitable course. The latter method was chosen for use in this work.

4. Selection of interpolation method

The identification of local maxima in a discrete signal is trivial and unambiguous. However, their connection is not trivial. There are many methods where none exist universal. It always depends on the situation. Most often you can meet with constant, linear, cubic or sinc interpolation. In our case, it seems appropriate linear and cubic. We will also use experimental ECI interpolation for comparison.

PLI - Piecewise Linear Interpolation

Linear interpolation is the simplest and fastest after constant interpolation. To determine the equation of a line between two points, it is enough to know the coordinates of the endpoints. In our case, we don't even have to know it, because we're looking for a global maximum, and that's it certainly located in an already known point.

CSI - Cubic Spline Interpolation

Cubic interpolation is the connection of points to 3rd degree polynomials that together form continuous function with continuous first and second derivatives. We distinguish natural, clamped and not-a-knot cubic interpolation. In our case we choose the type natural, which has the second derivative in the first and in the last segment equal to 0. Cubic interpolation is more complex than linear, each segment needs to solve a system of linear equations. It also depends on the amount interpolated points. More point means longer calculation, larger resulting data file, but also a more faithful signal reconstruction. Fewer points is faster, however the signal may be jagged. Therefore, it is important to choose the right compromise.

ECI - Extremum Center Interpolation

This interpolation method is mainly used to find the IMF components of the signal, however, it may be interesting to test it to evaluate the shift. Alternately proceeds through the found local maxima and minima. Always to one local extreme, a complementary point is found lying at the intersection of the vertical line and the line intersecting two opposite extremes. The centers of these points are then joined by a cubic interpolation.

5. Library implementation

C language is an ideal choice for solving similar problems. From the library required speed, determinism, and portability. If done correctly, the C language fulfills everything. The library is named shm_shift.c and is represented an shm_shift_t object that is of type * struct *. It is located in this structure all data. It is mainly an array of signal objects of type struct, which represent the analyzed signals, and the csv_parser object. Although it may seem that CSV file processing is trivial, it is unnecessary to reinvent the wheel when it can use a tested and functional solution, especially if it is only a support functionality.

The signal structure contains the signal name, input data points, local indexes extremes, interpolated points, centers of extremes, global maximum and minimum interpolated waveform, and in particular the shift of the signals from the reference in the x-axis.

The library interface can be divided into several logical units. It must first object to initialize, use the create function. Next, the CSV is typically read file, the data is analyzed and the result is written to CSV files. It will be used for this read_csv, analyze_csv, write_csv. Alternatively, the signal can be analyzed directly from data from memory using the analyze_signal function. It is necessary to finish correctly free dynamically allocated data to prevent memory leaks. Function dispose_calc releases analysis data and interpolated points, dispose_all except it also releases input data, and the free function eventually releases everything.

The library compiled with GCC takes up 27 KB. In addition to the standard language library C no external dependencies are used, so it can be integrated into different ones environments including embedded systems.

6. Use of the library

Use in the practical case should be straightforward and simple. It is a must have input data representing acoustic signals in the correct format in a CSV file, or ideally directly in memory in the signal structure. The data is in a CSV file stored in columns, where the first line is the text name of the signal and the next lines represent the values of the y-axis. X-axis data is not needed, assuming samples were taken equidistantly over time.

Example of input data in CSV format

Dref	D1	D2	D3	D4	D5
‒45	‒51	‒61	‒68	‒43	‒61
‒43	‒50	‒59	‒66	‒42	‒59
‒42	‒49	‒57	‒65	‒40	‒57

Example of using a library

char* file_in = "./data/data.csv"; /* input file */
char* file_out = "./data/result"; /* output files */
char delim = ';'; /* csv delimiter */
int ni = 10; /* number of interpolated points */
int ref_col = 0; /* number of reference signal column */

/** 1. create library object */
shm_shift_t* shm = shm_shift__create();

/** 2. read input data from CSV file */
int ret1 = shm_shift__read_csv(shm, file_in, delim);

/** 3a. analyse and write output CSV for PLI algorithm */
int ret2 = shm_shift__analyse_csv(shm, PLI, ref_col, 0);
int ret3 = shm_shift__write_csv(shm, file_out, delim);

/** 3b. dispose, analyse and write CSV for CSI algorithm*/
shm_shift__dispose_calc(shm);
int ret4 = shm_shift__analyse_csv(shm, CSI, ref_col, ni);
int ret5 = shm_shift__write_csv(shm, file_out, delim);

/** 4. finally clean up all */
shm_shift__free(shm);

In addition to the resulting interpolated waveforms, we are most interested in value shift_x_max. Of course, you can continue to work with it in C language and create it system for online SHM. In our case, it is enough to import the obtained data into MATLAB environment to work offline.

The resulting offset of a specific signal from the reference is now sufficient to subtract. Thus we plot the adjusted signal together with the reference one in a graph. If we chose appropriate test wave parameters, generated and measured it correctly, and selected appropriate interpolation method, we can determine from the graph whether the material has occurred to delamination.

Example of analysis of results in MATLAB environment

path = "../data/"; % directory with csv files
prefix = "data"; % prefix of those files
data = readtable(path + prefix + ".csv"); % read csv files
results_pli = readtable(path + prefix + "_results_pli.csv");
results_csi = readtable(path + prefix + "_results_csi.csv");

%% plot signals
for i = 2:size(data, 2)
    figure; % create figure
    x = i * 5; % shift_x_max is in multiples of five
    shift_pli = results_pli.(x); % get shift of PLI alg
    shift_csi = results_csi.(x); % get shift of CSI alg
    
    % plot data
    plot(1:size(data,1), data.(1)); % plot original signal
    hold on; % enable multiple plots
    grid on; % show grid
    plot((1:size(data,1)) - shift_pli, data.(i)); % plot PLI shifted sig.
    plot((1:size(data,1)) - shift_csi, data.(i)); % plot CSI shifted sig.
    
    % set figure properties
    name = data.Properties.VariableNames(i); % get sig. name
    title(string(replace(name, '_', '_{')) + "}"); % title
    xlabel('time'); % axis x label
    ylabel('value'); % axis y label
    legend('reference', 'shifted (PLI)', 'shifted (CSI)'); % legend
end

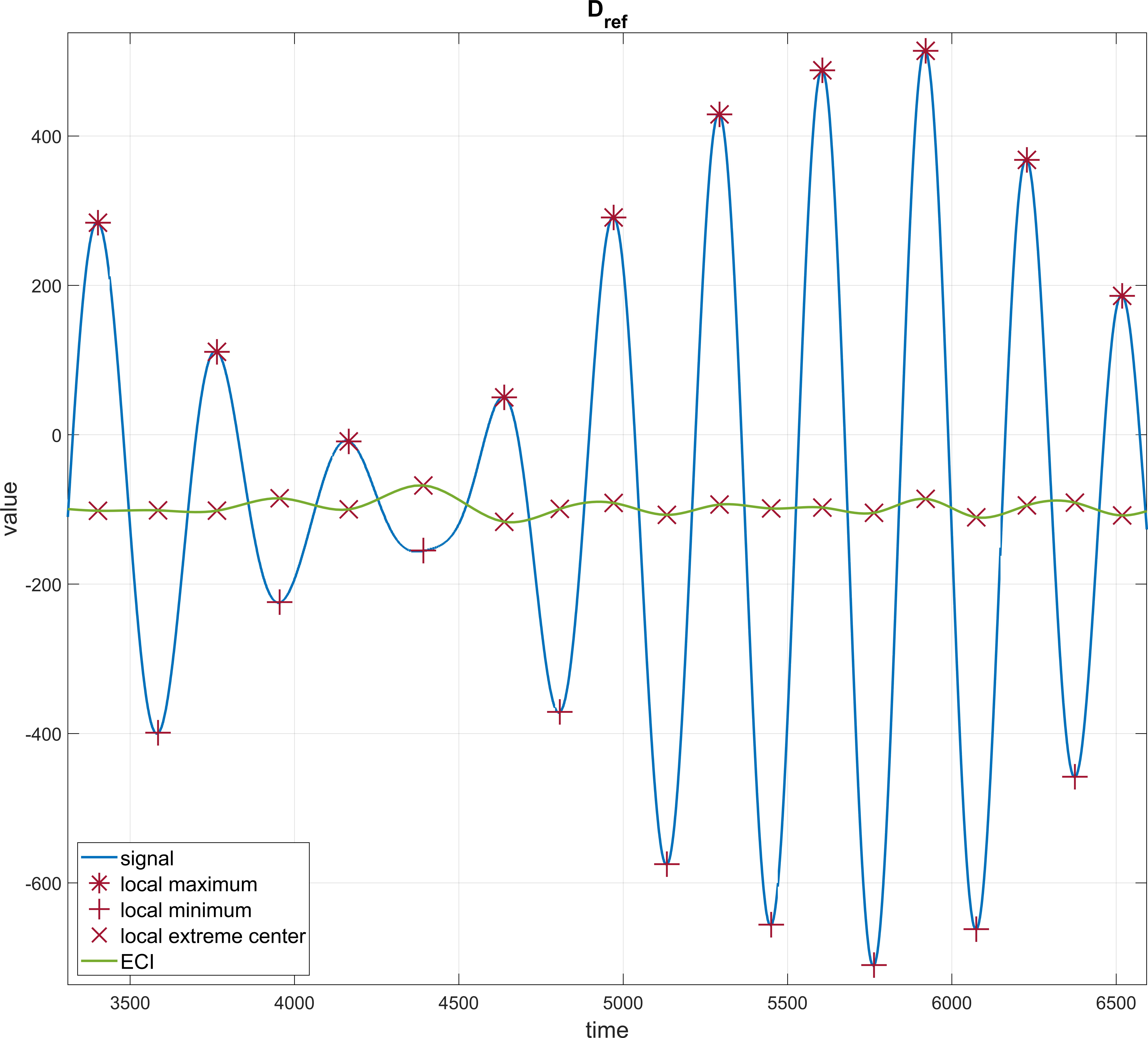
7. Analysis of used methods

The ECI method (Fig. 1) proved to be unusable. It determined in 6 out of 10 samples global maximum wrong. It has been confirmed to be particularly suitable for signal decomposition on IMF functions, for example in the Hilbert Huang transform.

Interpolation of centers of local extremes by ECI method (green).

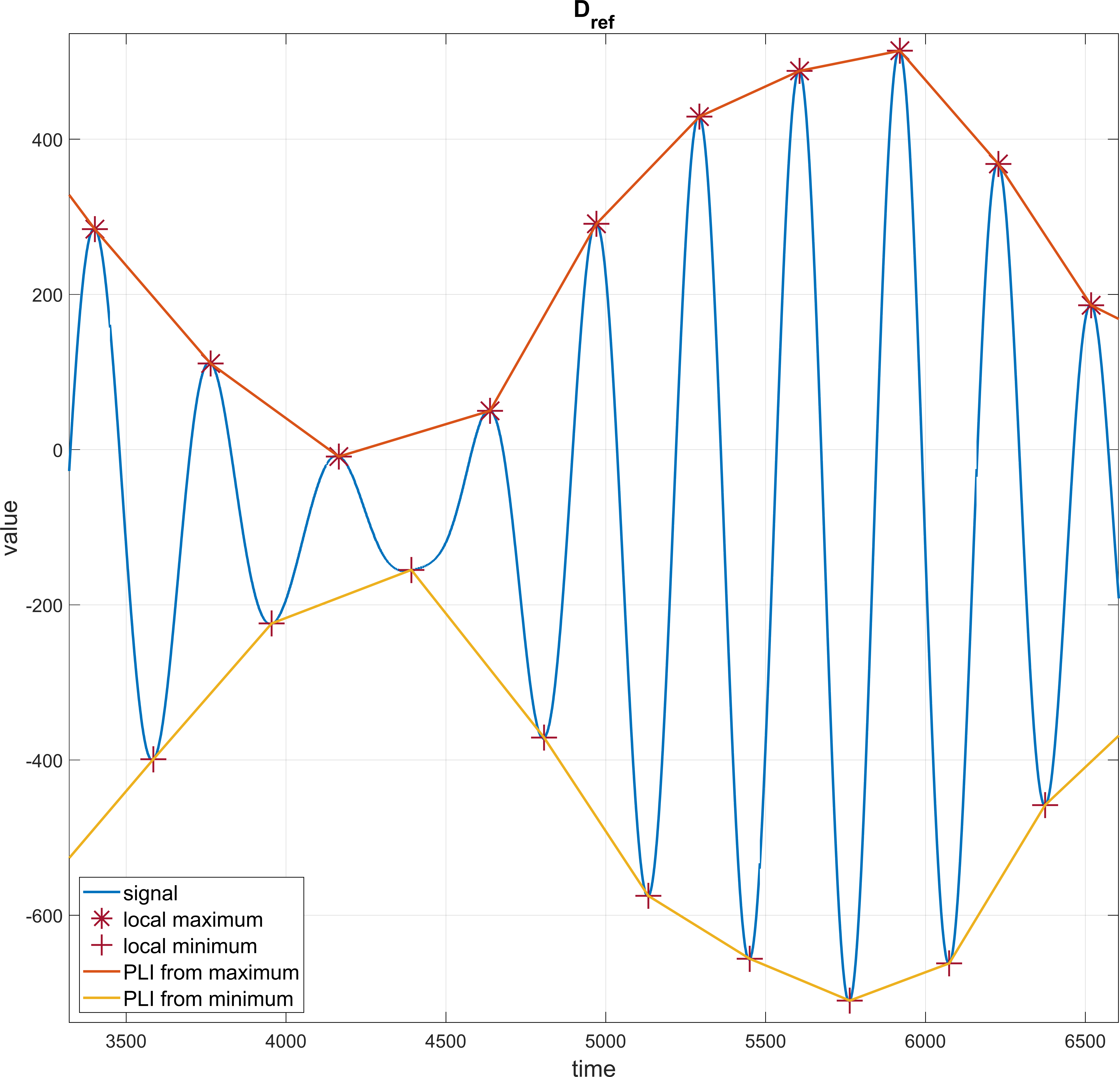
Linear PLI interpolation (Fig. 2) has its advantages especially in speed. The mean value of the reference signal of 10300 samples took to calculate at test PC (Intel i7 Ivy Bridge 2.7 GHz) with OS Linux Ubuntu about 13 µs. PLI interpolation on the same assembly lasted approximately 37 µs. However, it must be said that there is essentially no interpolation. As already mentioned, in the case of PLI it is enough to identify local extremes and global maximum from already available data points. There is no need to create another artificially. The resulting ratio of the algorithm calculation time with respect to the time of calculation of the mean value is 2.9. Unlike CSI and ECI, this value does not depend on the number of interpolated points.

Interpolation by PLI method. Orange indicates the connection of local maxima, yellow connection of local minima.

Comparison of library speed using different methods

ni	mean (μs)	PLI (μs)	CSI (μs)	ECI (μs)	PLI (coef.)	CSI (coef.)	ECI (coef.)
100	12.6	36.5	63.3	214.9	2.89	5.04	17.10
10	12.5	36.2	46.9	60.9	2.90	3.75	4.87
3	12.7	36.9	44.4	54.3	2.89	3.49	4.27
1	12.9	37.1	39.7	51.5	2.89	3.09	4.01

The stated values apply to a signal with 10300 samples. This is the average of 100 measurements. The column ni indicates the number of interpolated points and does not make sense for the PLI method. On the left is the duration in µs. In the right part is the ratio of duration to length the duration of the calculation of the mean value, which is given in the second column mean.

The CSI method is slower than the PLI by microsecond units, it provides incomparably better results. For 1 point, the calculation took about 40 µs and the coefficient of velocity was 3.1, for 10 points it was 46.9 µs and the coefficient was 3.8. For 100 interpolated points, the duration of the algorithm increased to 63.3 µs with a speed coefficient of 5.0. It might seem that amount interpolated points will significantly affect the overall speed. In fact, however these are units of microseconds. For online analysis (for example in embedded equipment) would certainly be a relevant factor, but in our case it does not play no role. The field size of the interpolated signal is directly proportional to what is discussed parameter ni, the specific value can be calculated as $$ \ left \ lbrack (1 + \ text {ni}) \ bullet \ text {pts} \ right \ rbrack - \ text {ni} $$. Amount interpolated points is marked as pts, in our case it is a number local maxima or minima, respectively.

From FIG. 3 it is obvious that 1 or 3 points are not insufficient for correct analysis. For specific input data, 100 points seems to be unnecessarily too much, therefore choose 10 points as the default value for further calculations.

CSI interpolation. The use of 1 interpolation point is marked in yellow, orange 3 points, black 10 points and green is marked PLI interpolation for comparison.

8. Identification of delamination

We now have almost everything we need to identify delamination tested material. We use the CSI method with 10 interpolation points and obtain global maximum signal envelope. In FIG. 4 you can see how it differs globally maximum when using the PLI and CSI methods. Linear interpolation provides a distorted notion of where the global maximum is actually located.

Comparison of the global maximum determined by the CSI method (orange square) and using the PLI method (yellow diamond on the right).

The shape of the resulting envelope is not important. To illustrate the form of ultrasound generated waves can be observed Fig. 5.

Test signal envelope generated by CSI method (black). For comparison PLI interpolation is highlighted in green and ECI interpolation in purple.

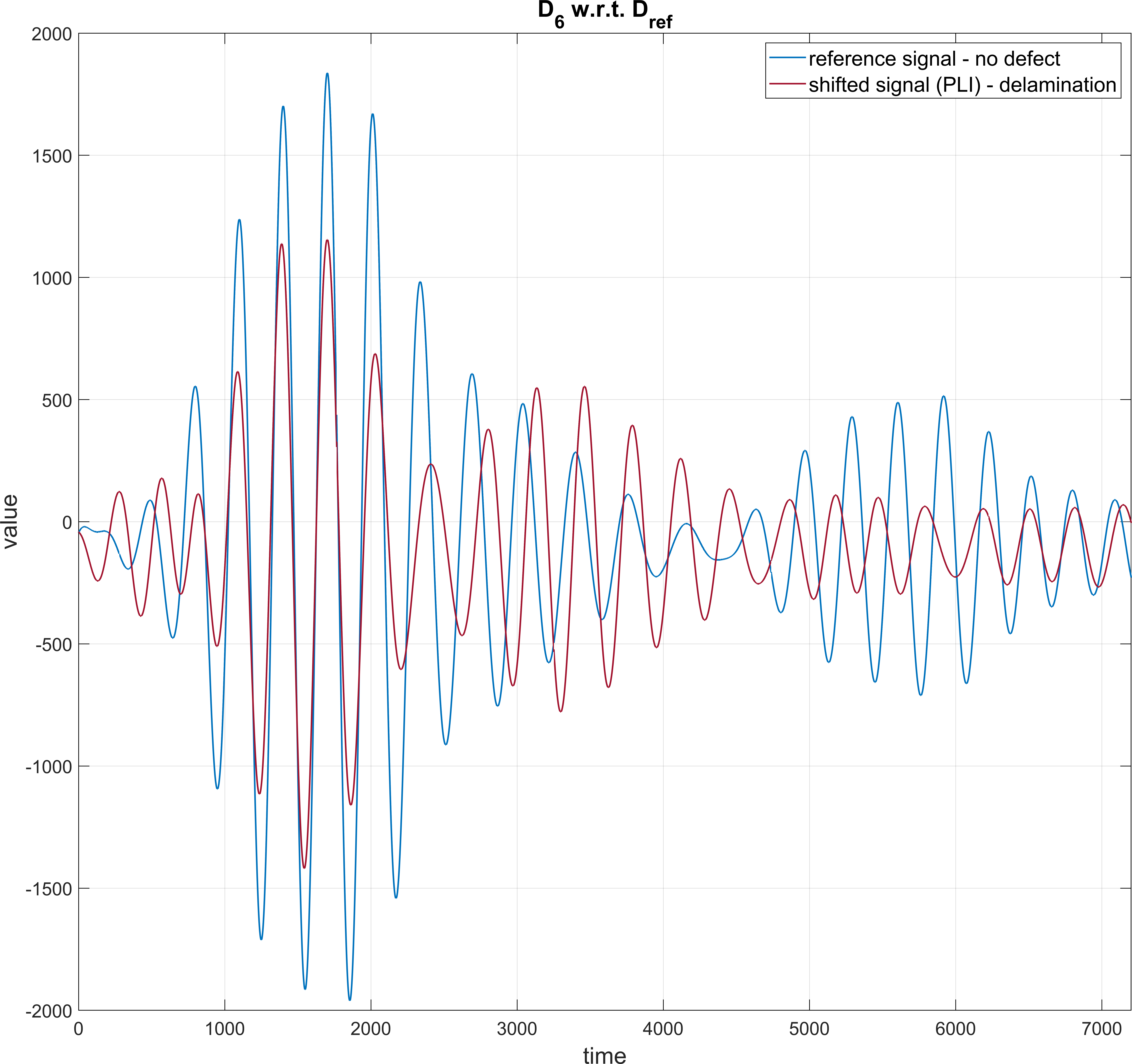
The last step is to subtract the obtained offset from the tested signal and clogging to the chart along with the reference. The interpolation method used is significantly reflected here, because it determines the global maximum from which the shift is calculated. When linear interpolation occurs due to inaccurate determination of the global maximum bias of results. The waves are aligned to the maximum value, which leads to incorrect localization of material delamination. This can be seen in Fig. 6. In the left part you can see the overlap of both waves, indicating the same rate of propagation and thus the absence of a defect, which is wrong, however, because it is a sample with the present delamination.

Inaccurate result of SHM analysis due to used PLI interpolation.

The correct determination of the global maximum or the shift of the signal from the reference is absolutely crucial for this ultrasonic SHM analysis. If an error occurs, it is then easy to draw bad conclusions from the resulting graphs. Therefore, it is necessary to choose interpolation method CSI and set the necessary parameters correctly. PLI and ECI methods they are for comparison and experimentation only.

The time on the x-axis corresponds to the propagation of the wave through the surface of the material from point A to point B. If we proceeded correctly, we have a reference wave (material without defects) and the tested wool (delamination material). In addition, we have both waves compared according to the global envelope maximum. This allows us to determine if and where it occurred to delamination of the composite material, because we know that the acoustic signal propagates at different speeds depending on the thickness of the material. Longitudinal propagation speed waves in solids depends on the ratio of wavelength and environmental dimensions. In practice it would still be necessary to compensate for the effect of temperature. Damaged (thinner) material, the wave will run faster. In FIG. 7 we can see delaminated (red) and reference (blue) sample. To determine a specific value delamination, we would need to know more data, at least the type of material and test wave frequency.

Result of SHM analysis with used CSI interpolation. Shift tested red waves against the reference blue indicates delamination of the composite material.

9. Conclusion

Ultrasonic SHM is one of the modern techniques with considerable potential for testing composite materials and detecting structural defects. There are many ways to align the reference and test sample. It would be interesting to compare the results of this method with, for example, the Hilbert transform or low-pass filtering. Cubic interpolation, or rather its global maximum, is, in my opinion, a quality and fast method that would definitely not lag behind others.

---

The developed library is usable for offline ultrasonic SHM testing, is however, it is necessary to use the CSI method with at least 10 interpolation modes. Pro online testing, it is necessary to implement the last step, which is indicated in this work in the MATLAB environment. After subtracting the displacement from the tested wave, subtract the resulting wave wave from the reference signal. The difference symbolizes a change in transit time waves through material with an anomaly and can be converted to millimeters, for example.

10. References

1. L. Michalcová and R. Hron, "Quantitative Evaluation of Delamination in Composites Using Lamb Waves ", IOP Conference Series: Materials Science and Engineering, vol 326, pp. 012006, 2018. Available: 10.1088 / 1757-899x / 326/1/012006 [Accessed 16 June 2020].

2. "Ultrasonic Testing", Nde-ed.org, 2020. [Online]. Available: www.nde-ed.org/EducationResources/CommunityCollege/Ultrasonics/. [Accessed: 16- Jun- 2020].

3. J. Šplíchal and J. Hlinka, "Modeling of health monitoring signals and detection areas for aerospace structures ", 13th Research and Education in Aircraft Design: Conference proceedings, 2019. Available: 10.13164 / conf.read.2018.17 [Accessed 16 June 2020].

4. Y. Yang, Signal Theoretic Approach for Envelope Analysis of Real-Valued Signals ", IEEE Access, vol. 5, pp. 5623-5630, 2017. Available: 10.1109 / access.2017.2688467.

5. E. Tarpara and V. Patankar, "Real time implementation of empirical mode decomposition algorithm for ultrasonic nondestructive testing applications ", Review of Scientific Instruments, vol. 89, no. 12, pp. 125118, 2018. Available: 10.1063 / 1.5074152.

6. Z. Liu and Z. Zhang, The Improved Algorithm of the EMD Decomposition Based on Cubic Spline Interpolation ", Signal Processing Research, vol. 4, no. 0, pp. 63, 2015. Available: 10.14355 / spr.2015.04.011.