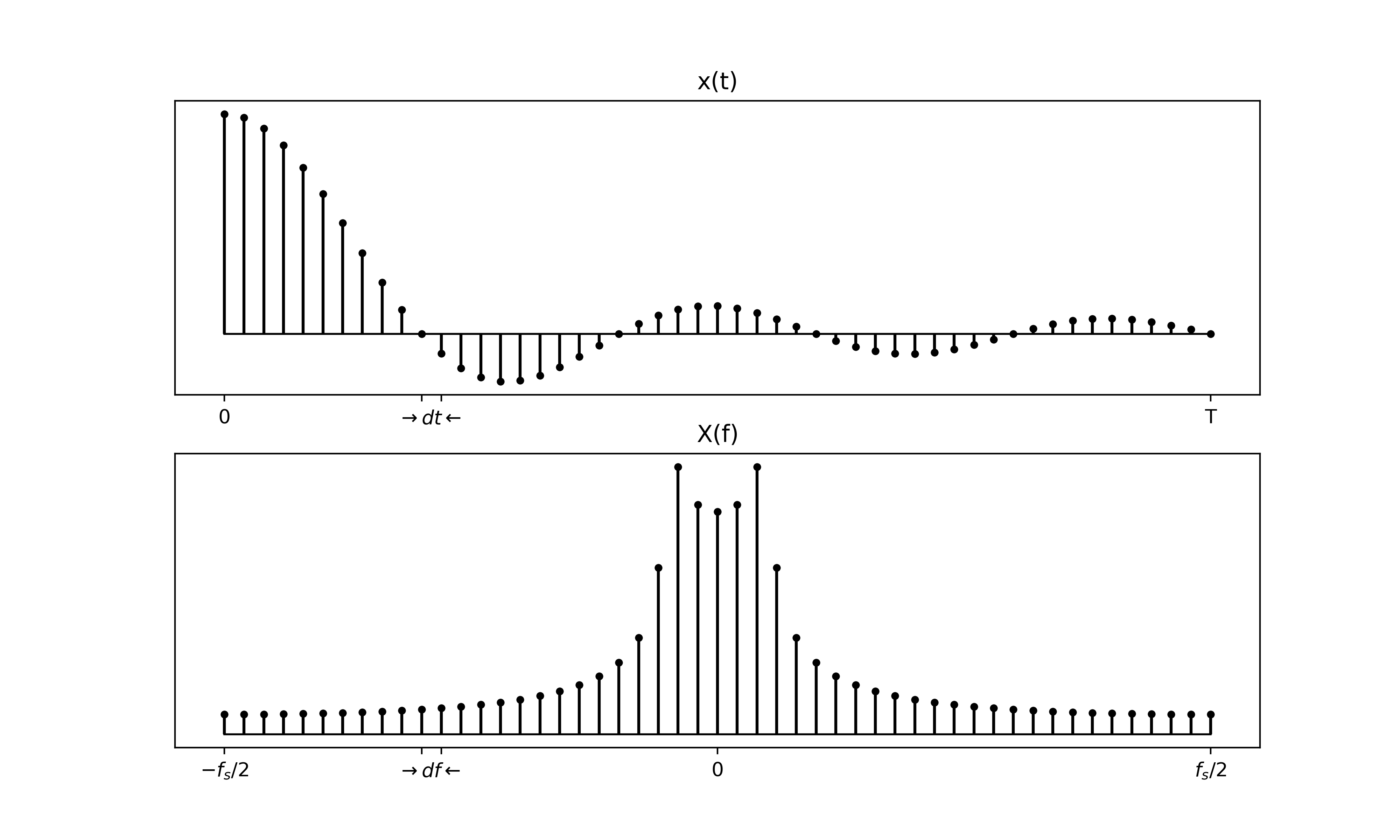
介紹時間與頻率的關係以及如何運用 numpy fft
- x(t) <--> X(f)
- sampling rate/frequency: fs
- 訊號長度: N
- 時間解析度: dt
- 頻率解析度: df
- N = T * fs
- N = T/dt = fs/df
由這兩條可以得出
- fs = 1/dt
- T = 1/df
中心思想是測不準原理,頻率與時間互為對偶。(跟動量、位置的測不準原理是同樣的數學模型)也就是說如果想要讓時間測準一點,頻率就會不準;頻率準一點,時間就會不準。
如果時間變為兩倍 (T->2T), fs, df 均變一半 (by 1., 4.)。
fs 變一半表示可以看到的高頻部分都會 aliasing 到低頻的部分,會影響結果。
df 變一半表示頻率解析度變高。
也就是說,拿 (0,2T) 的訊號去做傅立葉,你能看到的頻率上限降低一半,頻率解析度會增加。
如果時間變為兩倍 (T->2T) ,N 變兩倍 (by 1.),df 變一半 (by 4.)
N 變大表示訊號的傅立葉計算時間會變久,儲存量也變大。
df 變一半表示頻率解析度變高。
也就是說,如果我想讓頻率解析度較大,拿 (0,2T) 的訊號去做傅立葉,做出來的頻譜比較精細,但是你不會知道這些頻率是在 (0,T) 發生的還是 (T,2T) 發生的
- 如果今天需要測量的頻率為f,那 sampling frequency 至少要有 2f。
- 由 4. 式可知頻率的解析度取決於訊號 time domain 的長度。所以如果有人說他想要看出 10 Hz 與 12 Hz 的差距,但是她每次做傅立葉都只取 0.2 秒的時間,那他一定在唬爛。(至少要 0.5 s)
X_f = abs(np.fft.fftshift(np.fft.fft(x_t)))/Nfft: 做 fft。input, output array 長度皆為 N,output 頻率範圍為 (0, fs)fftshift: 搬一下 frequency domain 訊號。 (0, fs) -> (-fs/2, fs/2)abs: 原始運算完為複數,加了絕對值轉為實數。/N: FFT運算完振幅大小會是錯的,所以要除以訊號長度。
- fft 範例 source code
- 上面那張圖的 source code