You are choreographing a circus show with various animals. For one act, you are given two kangaroos on a number line ready to jump in the positive direction (i.e. toward positive infinity).
- The first kangaroo starts at location
x1and moves at a rate ofv1meters per jump. - The second kangaroo starts at location
x2and moves at a rate odv2meters per jump.
You have to figure out a way to get both kangaroos at the same location at the same time as part of the show. If it is possible, return YES, otherwise return NO.
x1 = 2
v1 = 1
x2 = 1
v2 = 2
After one jump, they are both at x = 3, (x1 + v1 = 2 + 1, x2 + v2 = 1 + 2), so the answer is YES.
Complete the function kangaroo in the editor below.
kangaroo has the following parameter(s):
int x1, int v1: starting position and jump distance for kangaroo 1int x2, int v2: starting position and jump distance for kangaroo 2
stringeitherYESorNO
A single line of four space-separated integers denoting the respective values of x1, v1, x2, and v2.
0 <= x1 < x2 <= 100001 <= v1 <= 100001 <= v2 <= 10000
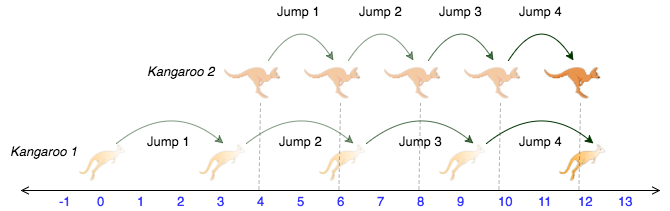
0 3 4 2YESThe two kangaroos jump through the following sequence of locations:
From the image, it is clear that the kangaroos meet at the same location (number 12 on the number line) after same number of jumps (4 jumps), and we print YES.
0 2 5 3NOThe second kangaroo has a starting location that is ahead (further to the right) of the first kangaroo's starting location (i.e., x2 > x1). Because the second kangaroo moves at a faster rate (meaning v2 > v1) and is already ahead of the first kangaroo, the first kangaroo never be able to catch up. Thus, we print NO.