Replies: 6 comments 1 reply
-
|
For me this plot 6D, radiation ON, should give the "saw tooth", horizontal orbit slowly oscillating to negative values, and recovering at the RF cavities. This is order of micrometers for esrf. I tried the code that you propose and also |
Beta Was this translation helpful? Give feedback.
-
|
Hello @lnadolski , I confirm your result for the esrf lattice from this AT This is what is expected, I do not know this |
Beta Was this translation helpful? Give feedback.
-
|
Ah @simoneliuzzo has the same answer, well synchronized! @simoneliuzzo do you know of any problem with this lattice? Wasn't there an issue with the total bending angle? |
Beta Was this translation helpful? Give feedback.
-
|
This is strange. |
Beta Was this translation helpful? Give feedback.
-
|
This is in fact strange... are the passmethods the same in all these lattices? |
Beta Was this translation helpful? Give feedback.
-
|
Dear colleagues, After looking more into this issue, I think it is somehow a feature of multi bend lattices to have a clearly recognizable sawthoot effect. We may expect larger 6D orbit for DBA/TBA lattices compared to MBA. For the upgrades dispersion is smaller as well as energy loss, so the orbit due to delta-vs-s is smaller (max(delta)*max(disp) ~ 8um for EBS, ~140 um for ESRF-DBA). I have done several tests and among them I fixed the geometry of the esrf.m lattice that is slightly wrong as suggested by @carmignani. (I attach here a file with corrected angles in all dipoles to close the geometry). For the 6D orbit I do not see changes, and I am convincing myself that it is the correct orbit. I try to place 1 cavity in each cell of the DBA esrf lattice. The expectation is that the energy changes are smaller, thus we should see smaller over all 6D orbit and a zig/zag, dispersive pattern with positive orbit in the first half (higher energy) of the cell and negative in the second half (lower energy). |
Beta Was this translation helpful? Give feedback.





-
Dear All,
Computing the closed orbit in 6D with radiation ON, I am puzzled by the amplitude in the horizontal plane which can reach 100µm.
I take the example of esrf lattice in the following plot
atplot(atenable_6d(esrf,'auto'), @plClosedOrbit)
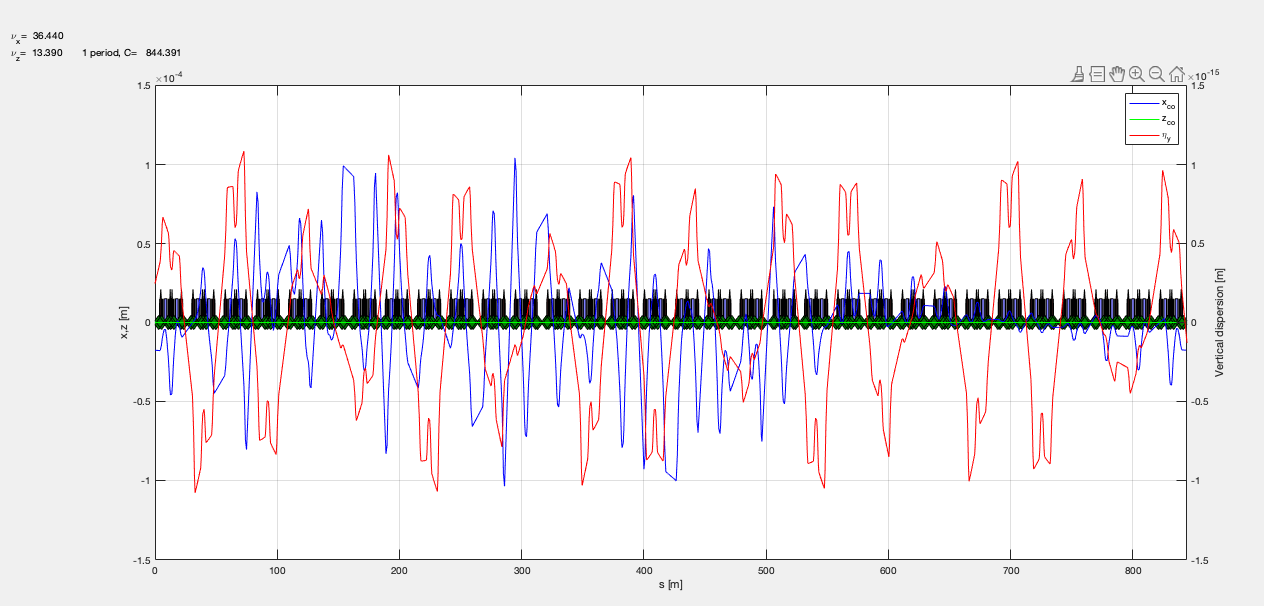
Does it make sense for you to you?
The averaged energy loss per turn is 8.0773e-04.
Laurent.
Beta Was this translation helpful? Give feedback.
All reactions