Репозиторій: https://github.com/archy-co/imss_sort_algs.git
У цій роботі було реалізовано 4 алгоритми сортування - Сортування вставкою, Сортування об’єднанням, Сортування вибором та Шел сорт - і порівняно їхню ефективність за часом роботи та кількістю порівнянь у 4 різних випадки:
- Випадковий масив (було проведено 5 експериментів і взято середнє значення). Максимальне значення у масиві - розмір масиву + 1
- Висхідний масив з уже відсортованими значеннями. Максимальне значення - розмір масиву + 1
- Низхідний масив зі значеннями, відсортованими у зворотному порядку. Максимальне значення - розмір масиву + 1
- Випадковий низький масив - містить лише елементи з набору {1, 2, 3} - тобто масив з багатьма повторюваними елементами (було проведено 3 експерименти і взято середнє значення)
Кожен з 4 алгоритмів виконувався у всіх згаданих вище 4 випадках для масивів розміром 2^7, 2^8, .. до 2^15 включно (крок розміру масиву = 2)
Результатом експериментів є графіки, побудовані за допомогою matplotlib
Зауважте, що для запису часу алгоритму та кількості порівнянь використовуються різні алгоритми: при записі часу використовується оптимізований алгоритм без будь-яких, однак для при підрахунку кількості порівнянь використовується дещо змінена версія алгоритмів (із суфіксом _verb у назві) з лічильник порівнянь.
Експерименти були проведені з такими ключовими апаратними параметрами:
- Процесор: процесор Intel Core i5-10210U з тактовою частотою 1.60 ГГц, 8 ядер
- Памʼять: SO-DIMM 8 ГБ @ 2666 МГц
- ОС: Linux (I use Arch, btw)
Наступний код написаний на C++. Докладніше див. у файлах src/insertion_sort.cpp, src/merge_sort.cpp, src/selection_sort.cpp, src/shell_sort.cpp та пов’язаних з ними файлах
void insertion_sort(int* arr, int size){
for(int i = 1; i < size; i++){
for(int j = i; j > 0; j--){
if(arr[j] < arr[j-1]) {
int temp = arr[j];
arr[j] = arr[j-1];
arr[j-1] = temp;
}
}
}
}void merge_sort(int* arr, int l, int r){
if(r > l){
int m = l + (r - l) / 2;
merge_sort(arr, l, m);
merge_sort(arr, m + 1, r);
merge(arr, l, m, r);
}
}void merge(int* arr, int l, int m, int r){
int arr_l_p = m-l+1, arr_r_p = r-m;
int arr_l[arr_l_p], arr_r[arr_r_p];
for(int i = 0; i < arr_l_p; i++) arr_l[i] = arr[l+i];
for(int i = 0; i < arr_r_p; i++) arr_r[i] = arr[m+1+i];
int i = 0, j = 0, n = l;
while(i < arr_l_p && j < arr_r_p){
if(arr_l[i] <= arr_r[j]) {
arr[n] = arr_l[i];
i++;
}
else{
arr[n] = arr_r[j];
j++;
}
n++;
}
while(i < arr_l_p){
arr[n] = arr_l[i];
n++, i++;
}
while(j < arr_r_p){
arr[n] = arr_r[j];
n++, j++;
}
}void selection_sort(int* arr, int size){
int min_ind = 0;
for(int i = 0; i < size; i++){
min_ind = i;
for(int j = i+1; j < size; j++){
if(arr[j] < arr[min_ind])
min_ind = j;
}
int temp = arr[i];
arr[i] = arr[min_ind];
arr[min_ind] = temp;
}
}void shell_sort(int* arr, int size){
for (int gap = size/2; gap > 0; gap /= 2) {
for (int i = gap; i < size; i++) {
int temp = arr[i];
int j = i;
for (; j >= gap && arr[j - gap] > temp; j -= gap)
arr[j] = arr[j - gap];
arr[j] = temp;
}
}
}Функція expsFuncs виконує експерименти та записує дані експерименту у файл Код нижче пропускає деякі важливі нюанси, такі як імпорт або декларація/визначення деяких констант і функцій. Докладніше див. у файлах src/experiment.cpp репозиторію. Модифікації алгоритмів, які підраховують порівняння, реалізовані в src/algorithm_name.cpp нижче основного алгоритму у файлі.
#define EXPERIMENTS_COUNT 4
#define FUNCS_COUNT 4
// sort_algs is an array of optimized functions that sort an array
void (*sort_algs[])(int*, int) = { selection_sort, insertion_sort, merge_sort, shell_sort };
// sort_algs_verb is an array of funcitons that sort an array and return number of comparisons
long (*sort_algs_verb[])(int*, int) = { selection_sort_verb, insertion_sort_verb, merge_sort_verb, shell_sort_verb };
// fill_types is an array of functions that generate arrays (random array, ascending array, descending array, and random array of set {1, 2, 3})
void (*fill_types[])(int*, int) = { randArr, ascArr, descArr, randLowArr };
// how many times each of experiments will be performed (random array will be performed 5 times and average will be taken; random array of set {1, 2, 3} is performed 3 times; in 2 other cases- only once)
const int FILL_TYPE_EXPERIMENT_REPS[EXPERIMENTS_COUNT] = { 5, 1, 1, 3 }; // different experiments repetition
void performExperiment(){
for(int i = 7; i <= 15; i++){
long res[EXPERIMENTS_COUNT][FUNCS_COUNT][2] = {};
expsFuncs(res, pow(2, i));
}
}
void expsFuncs(long res[EXPERIMENTS_COUNT][FUNCS_COUNT][2], const int size){
// Three arrays are used: arr_init is changed only once initialized,
// arr1 is sorted and time is recorded,
// arr2 is sorted and number of comparisons is recorded.
// arr1 and arr2 are initalized to be equal to arr_init on each round
int arr_init[size], arr1[size], arr2[size];
for(int k = 0; k < EXPERIMENTS_COUNT; k++){
for(int i = 0; i < FILL_TYPE_EXPERIMENT_REPS[k]; i++){
(fill_types[k])(arr_init, size);
for(int j = 0; j < FUNCS_COUNT; j++){
copy(arr_init, arr_init+size, arr1);
copy(arr_init, arr_init+size, arr2);
auto start = chrono::high_resolution_clock::now();
(sort_algs[j])(arr1, size);
auto stop = chrono::high_resolution_clock::now();
long duration = (chrono::duration_cast<chrono::microseconds>(stop - start)).count();
long comparisons = (sort_algs_verb[j](arr2, size));
res[k][j][0] += duration;
res[k][j][1] += comparisons;
}
}
for(int i = 0; i < FUNCS_COUNT; i++) {
res[k][i][0] /= FILL_TYPE_EXPERIMENT_REPS[k];
res[k][i][1] /= FILL_TYPE_EXPERIMENT_REPS[k];
}
}
} |
 |
|---|
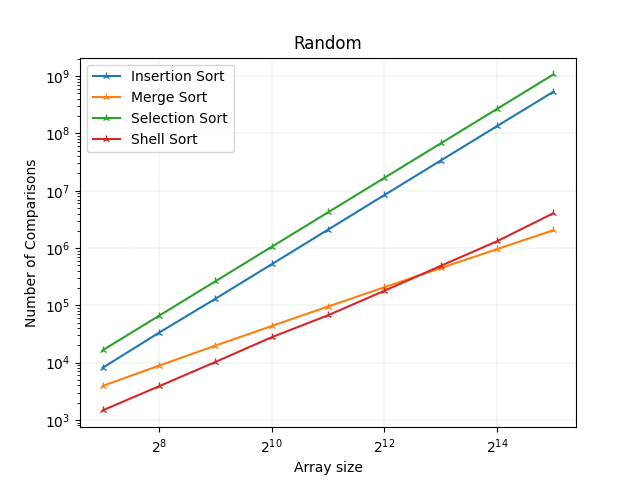
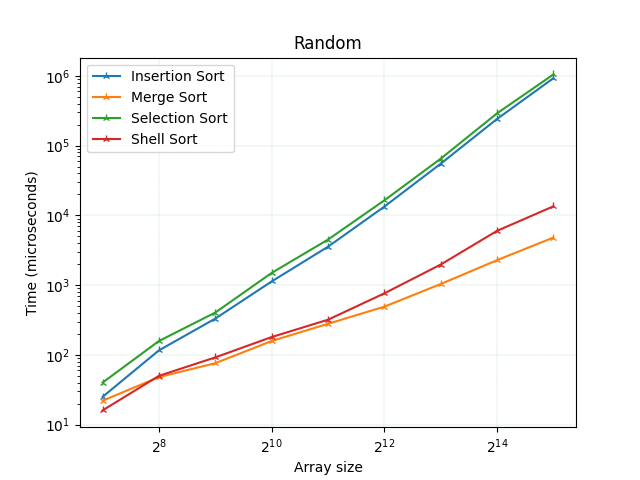
Сортування виділення дещо повільніше, ніж сортування вставки, але на загал корелює з ним. Далі йде шел сорт. До деякого розміру масиву (у наведених експериментах до ~ 2^12) він має менше порівнянь і має кращий час виконання, ніж сортування злиттям, але коли розмір масиву стає ~ 2^12, то сортування злиття стає кращим, а шел сорт починає все швидше і швидше зростати, віддаляючись від продуктивності алгоритму сортування злиттям.
 |
 |
|---|
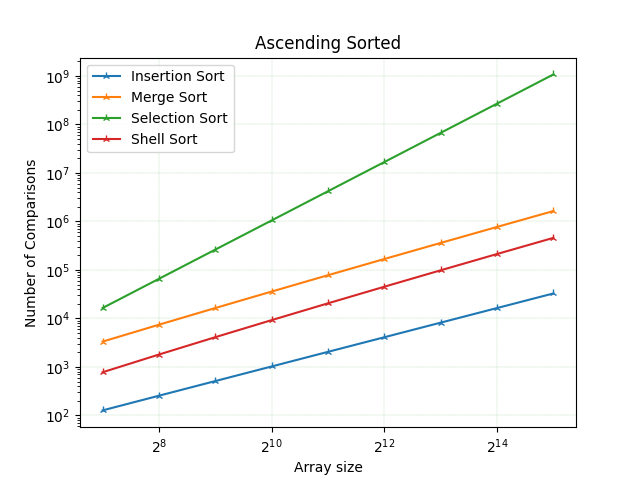
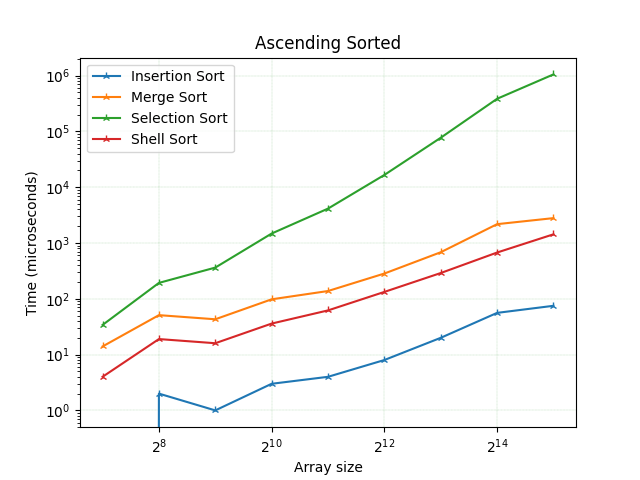
Сортування вставки завжди є найкращим у цьому випадку, оскільки має найменше порівнянь та найкращий час виконання. Далі, шел сорт - він заснований на сортуванні вставкою, тому він також досить швидкий і є другим найшвидшим серед усіх 4 алгоритмів за часом та кількістю порівнянь. Потім йде сортування злиттям і найгіршим є сортування вибору.
 |
 |
|---|
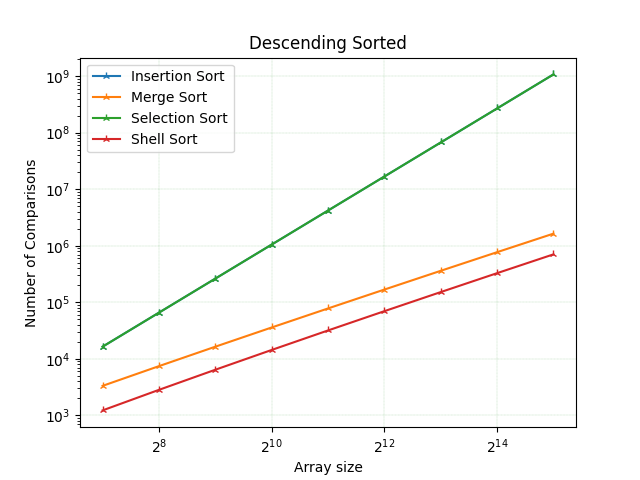
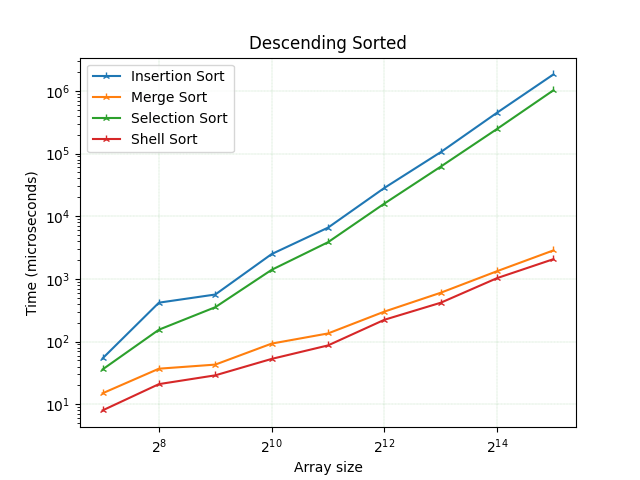
У цьому випадку сортування вставкою та сортування вибором мають найгірший час виконання та кількість порівнянь, які рівні для обох, оскільки обидва будуть виконувати n^2 порівняння для сортування масиву із зворотним порядком. Краща продуктивність у це сортування злиттям, а найкраща - у шел сорту.
 |
 |
|---|
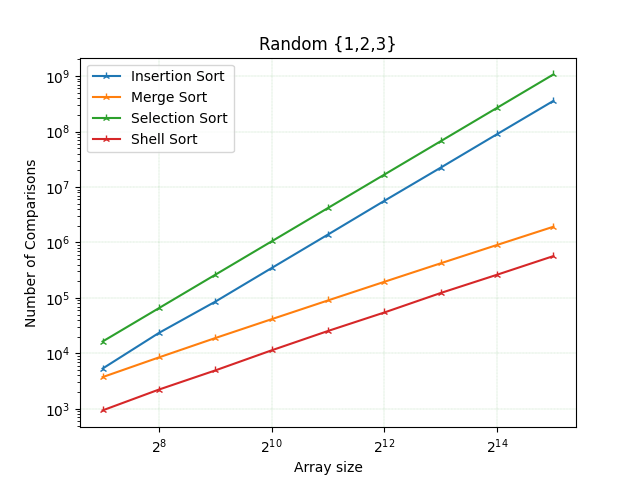
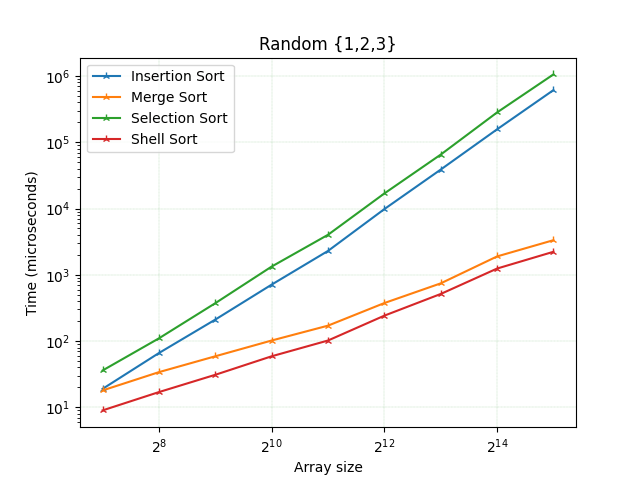
Час виконання та кількість порівнянь цього експерименту корелює з результатами сортування у випадковому масиві. Однак для даних розмірів масивів шел сорт завжди найкращий і працює краще, ніж сортування злиттям. Сортування вставки - третій найкращий, а найгірший - сортування за вибором.
Отже сортування відбором виконує в кожному експерименті найбільшу кількість порівнянь і працює протягом найдовшого періоду часу. Продуктивність сортування вставки є найкращою лише у випадку, якщо масив уже відсортований. У більшості інших випадків сортування злиттям та шел сорт значно кращі, ніж у попередні два алгоритми, і зазвичай вони близькі один до одного по результату. Однак для масиву з випадкових чисел сортування злиттям стає кращим починаючи з деякого розміру масиву (у проведеному експерименті цей розмір масиву становив ~ 2^12). Тим часом кількість порівнянь шел сорту прогресивно збільшується. Однак Шел сорт працює краще для масивів з багатьма повторюваними елементами.