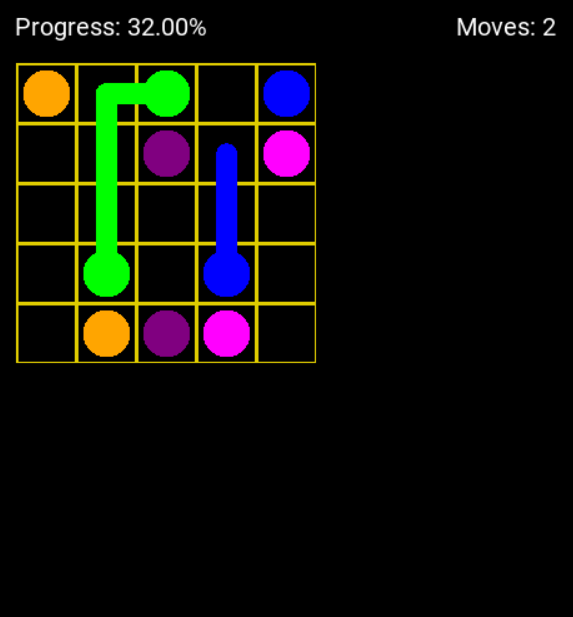
This project is a homage to the Flow Free game developed by Big Duck Games. The game allows you to play pre-configured levels, create your own grids or even play totally random grids!
Take a look at the docs for more information about the project.
The game is developed for computers with a minimum screen resolution of 1024x768. It is developed in Python 3.10 using the PyGame library.
- Python 3.10
- PyGame 2.1.2
The steps are to be executed in the PowerShell.
- Clone the repository
git clone https://github.com/amoralesc/flow.git
cd flow- Create a virtual environment
python -m venv venv- Activate the virtual environment
venv/Scripts/activateIf the above step fails, you may need to active the script execution policy:
Set-ExecutionPolicy -ExecutionPolicy RemoteSigned -Scope CurrentUser- Install the dependencies
pip install -r requirements.txtThe steps are to be executed in the terminal.
- Clone the repository
git clone https://github.com/amoralesc/flow.git
cd flow- Create a virtual environment
python -m venv venv- Activate the virtual environment
source venv/bin/activate- Install the dependencies
pip install -r requirements.txtBefore running the game, let's first take a look on how the grid is configured. A grid configuration is a JSON file that contains the initial state of the grid. For example, the grid configuration of the above screenshot is the following:
{
"rows": 5,
"cols": 5,
"qpoints": 5,
"points": [
[
[0, 0],
[4, 1]
],
[
[0, 2],
[3, 1]
],
[
[0, 4],
[3, 3]
],
[
[1, 2],
[4, 2]
],
[
[1, 4],
[4, 3]
]
]
}Take a look at the available run options by executing the following command:
python main.py -hThere are currently 25 levels pre-configured. These levels guarantee that there is always an unique solution to the grid.
Take a peek at the levels
cat data/levels.jsonTo play a level, run the following command:
python main.py -l LEVELwhere LEVEL is the level number (1-indexed position in the levels file).
You can also define your own grid configuration file. An example is provided here. Fair warning: the game does not check if the grid is solvable.
To play a grid from a file, run the following command:
python main.py -f FILEwhere FILE is the path to the grid configuration file.
You may also play a totally random grid. The grid will be generated by the game but it is not guaranteed that there is a solution to the grid.
To play a random grid, run the following command:
python main.py -r ROWS COLS QPOINTSwhere ROWS is the number of rows, COLS is the number of columns and QPOINTS is the number of points in the grid.
The Flow game is a numberlink-like game. This means that solving the game is an NP-complete problem. However, there are some heuristics that can be used to find an approximate solution to the game.
The solver implemented in this project is a modified version of the A* algorithm. That said, the solver is not guaranteed to find a solution to the grid, even if there is one (or more).
To run the solver, accompany any of the above commands with the -s flag. For example, to run the solver on the level 1, run the following command:
python main.py -l 1 -sYou may also activate debug mode by adding the -d flag. This will show the steps taken by the solver to find a solution to the grid.
python main.py -l 1 -s -dOf the current 25 levels, the solver is able to find a solution to 20 of them. It fails to find a solution to the following levels:
- Level 17: 8x8 grid with 6 point-pairs
- Level 19: 8x8 grid with 7 point-pairs
- Level 20: 8x8 grid with 6 point-pairs
- Level 22: 9x9 grid with 8 point-pairs
- Level 24: 9x9 grid with 7 point-pairs
The solver has a few parameters that can be tweaked to improve the performance of the solver. These parameters are defined in the config.py file. The parameters are:
MAX_REPETITIONS: maximum number of repeated paths the solver can find for a single point-pair before it backtracks. If the solver does not find a solution after this number of repetitions, it will backtrack to the previous point-pair.WINDOW_REPETITION: minimum number of repeated paths the solver must find for a single point-pair before it backtracks. For the example:- paths: 1, 2, 3, 4, 5, 6, 7, 8, 9
- current window size: 3
- window repetitions: 3
- The solver will check if [7, 8, 9] equals [4, 5, 6] and if [4, 5, 6] equals [1, 2, 3]. This is to determine if the current window size is repeated enough times to backtrack.
This project is licensed under the MIT License - see the LICENSE file for details.