This is a github repository of python code for Two-stream instability based on PIC method. The baseline code referred is from Philip Mocz. See the github link for original code of Philip Mocz. For the faster computation in field solver, Tri-diagonal Gaussian elimiation method is utilized for 1-dimensional two-stream instability simulation. For initial condition, we applied adding beam velocity with reversion of the sign in half of electrons, then applying the sinusoidal perturabtion in overall electron velocity distribution.
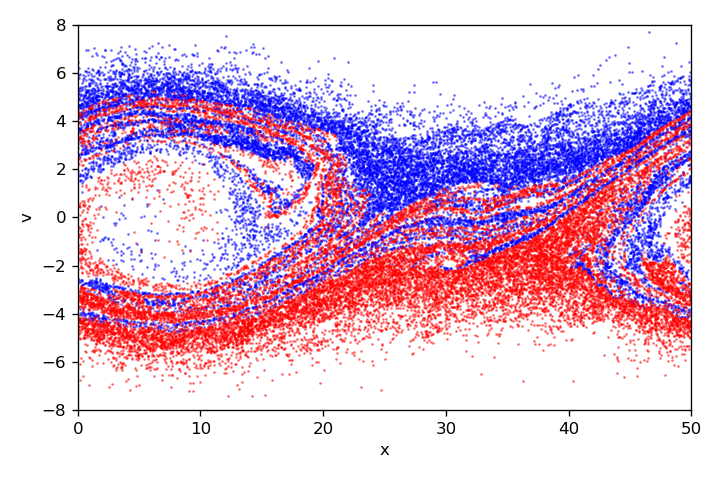
We developed two-stream instability simulation for 1D case using PIC method. The below shows the result of 1D case with leapfrog method (left) and implicit midpoint method (right).
In this code, we assumed 1D space with periodic condition for solving electrostatic electron plasmas with applying the velocity perturbation. Two different beam streams of plasmas shows interesting motion of electrons as you can see above. I will develop more complex situations including 2D case and develop the code based on parallel computation. Since the explicit leapfrog method is not a symplectic integrator, we also developed implicit midpoint method for preserving hamiltonian. The below describes two different results obtained from leapfrog (left) and implicit midpoint method (right).
The hamiltonian computed for each step shows that implicit midpoint method has better performance in terms of energy conservation compared with explicit method.
This code also simulates any initial condition which is given by any probability distribution. Rejection sampling is used to select random particles following the distribution, while the SOR algorithm is applied for stable computation during the simulation. The example below is a "Bump-on-tail" distribution with externel electric field. The analytic solution is already known, thus we compare two results from analytic solution (left) and PIC simluation (right).
- Create Your Own Plasma PIC Simulation, Philip Mocz
- Jianyuan XIAO et al 2018 Plasma Sci. Technol. 20 110501
- Hong Qin et al 2016 Nucl. Fusion. 56 014001