This dataset is comprised of simulation and hardware trajectories with various faults for the Digit robot during the task of standing. The simulation trajectories contain abrupt, incipient, and intermittent faults, while the hardware trajectories contain abrupt and incipient faults.
Digit_Dataset.mp4
- Repository Organization
- Installation
- Downloading the Dataset
- Loading the Dataset
- Dataset Information
.
├── c_function
| ├── CMakeLists.txt
├── utils
│ ├── DynamicsCalculator.py
│ ├── dataset.py
│ ├── params.yaml
└── README.md
└── main.py
└── .gitignore
-
Clone the repository
git clone https://github.com/UMich-BipedLab/Digit_Fall_Prediction_Dataset.git OR git clone git@github.com:UMich-BipedLab/Digit_Fall_Prediction_Dataset.git -
Generate shared libraries
-
Download the c_kin and extract it inside the c_functions folder.
-
Build the downloaded c functions:
# create a build folder cd Digit_Fall_Prediction_Dataset && cd c_functions mkdir build # build libraries cd build cmake .. make all
- Install python requirements
# create a virtual environment of your choice cd Digit_Fall_Prediction_Dataset && mkdir .venvs && cd .venvs python3 -m venv digit_venv source digit_venv/bin/activate pip3 install --upgrade pip # install python requirements cd .. pip3 install -r requirements.txt
Download the digit data folder and extract it in Digit_Fall_Prediction_Dataset root folder. Keep the folder name as digit data.
# create the DatasetLoader class
dl = DatasetLoader()
# load the dataset
dl.load_dataset(transform_real_trajectories=True, remove_hardware_data_after_killed=True, subtract_initial_angle_sim=True)
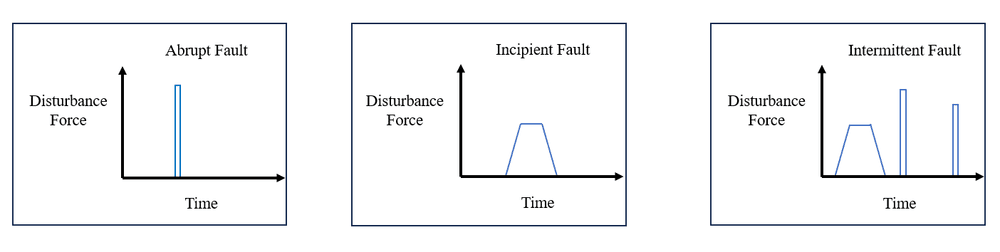
Falls can be attributed to faults, which are defined as unforeseen deviations in one or more operation variables. As depicted in Figure 1, faults can be classified into three types based on their time dependency: abrupt, incipient, and intermittent. Abrupt faults are rapidly varying, incipient faults are drift-like, and intermittent faults are sporadic. As we discuss in [1] each of these fault types can arise during real-world operation.
Relevant Definitions:
-
Critical faults: faults that lead to falls
-
Lead time: the time to react
- Defined as the difference between the time of the actual fall and the predicted fall
-
Unsafe trajectories: trajectories with critical faults
Figure 1
To generate the trajectories, we employ Agility’s MuJoCo-based simulator in conjunction with a standing controller [2]. The objective of the controller is to maintain both the center of mass and the zero-moment point within the support polygon. The faults are simulated by applying forces of various magnitudes to the robot’s torso in the x-direction (i.e., sagittal plane). To simulate minor disturbances that might induce slight oscillations in the robot’s standing posture, we introduce impulsive forces with a 0.075s duration, ranging from 0 - 202.4N, at the start of each trajectory.
Abrupt faults are simulated using impulsive forces with a duration of 0.075s, randomly uniformly distributed within a range of 0 - 414.8N. The range is chosen such that half of the trajectories contain critical abrupt faults. The impulsive forces are introduced randomly within a period of 1.5s, and a total of 900 trajectories were simulated.
Incipient faults are simulated with trapezoidal force profiles, as depicted in Figure 2. These profiles have a slope of 480N/s over a varying duration to result in a desired constant amplitude over a time duration of 1s; the resulting force amplitudes of incipient faults are randomly uniformly distributed between 0 - 57.6N. The range is chosen such that half of the trajectories contain critical abrupt faults, and the incipient faults are introduced randomly within a period of 1.5s. A total of 900 trajectories were simulated
Figure 2
Emulating the unpredictable nature of intermittent faults, we apply two distinct forces. These forces are designed to mimic either abrupt or intermittent faults. The first force’s magnitude remains within the safe range, while the second force’s magnitude can potentially lead to a fall or maintain stability. Similar to the abrupt and incipient faults, the two forces are each applied randomly within a period of 1.5s. The time between the periods of application of the two forces is 2s. For instance, if the period of application for the first force is between 8.0 - 9.5s, the second force is applied between 11.5 - 13.0s.
To prevent the Digit robot from getting damaged during data collection, the hardware data generation is carried out with Digit attached to a gantry. Additionally, the motor power is “killed” when the robot starts to fall, thereby allowing the gantry to catch it. Note that we attempt to “kill” the motors prior to the gantry catching the robot. Impulsive and trapezoidal forces are introduced to the robot’s torso by pushing Digit with a pole. To emulate the trapezoidal forces that result in an incipient fault, the pole is first rested on Digit before pushing. Twenty-seven (27) safe and 13 unsafe trajectories are collected for abrupt faults, while 26 safe and 15 unsafe trajectories are collected for incipient faults. Figure 3 depicts the experimental setup of the hardware data.
Figure 3
The world frame is defined as the Digit's base pose (position and orientation) when it is powered on. During hardware data collection, after powering the robot on, it is positioned in its mark (as seen by the alignment of the Digit's toes to the blue tape on the ground in Figure 3). To ensure that the data collected is with reference to the Digit's starting pose as shown in Figure 3 instead of the world frame, a homogenous transformation is performed on the data collected. For implementation details, please refer to transform_real_trajectories() function in the ./utils/dataset.py file.
A simple Vizualisation program is provided to observe a specified trajectory of the digit robot. Specifiy the name of the trajectory and run the visualize function in main.py (e.g. python3 main.py). Ensure that the specified trajectory is loaded by dataset.py.
- M. E. Mungai, G. Prabhakaran, and J. Grizzle, “Fall Prediction for Bipedal Robots: The Standing Phase,” arXiv preprint arXiv:2309.14546 (2023), Submitted to ICRA 2024.
- G. Gibson, “Terrain-aware bipedal locomotion,” Ph.D. dissertation, University of Michigan, 2023.