261.graph_valid_tree.md

261. Graph Valid Tree

中等

https://leetcode-cn.com/problems/graph-valid-tree/

You have a graph of n nodes labeled from 0 to n - 1. You are given an integer n and a list of edges where edges[i] = [ai, bi] indicates that there is an undirected edge between nodes ai and bi in the graph.

Return true if the edges of the given graph make up a valid tree, and false otherwise.

Example 1:

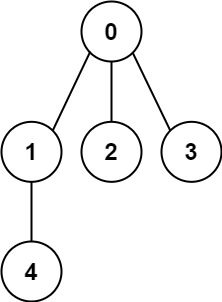
Input: n = 5, edges = [[0,1],[0,2],[0,3],[1,4]]
Output: true

Example 2:

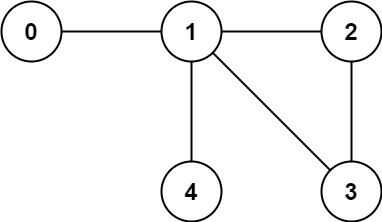
Input: n = 5, edges = [[0,1],[1,2],[2,3],[1,3],[1,4]]
Output: false

Constraints:

1 <= n <= 2000
0 <= edges.length <= 5000
edges[i].length == 2
0 <= ai, bi < n
ai != bi
There are no self-loops or repeated edges.

相关企业

• 领英 LinkedIn|8
• 谷歌 Google|3
• 亚马逊 Amazon|2
• 微软 Microsoft|2

相关标签

• Depth-First Search
• Breadth-First Search
• Union Find
• Graph

相似题目

• Course Schedule 中等
• Number of Connected Components in an Undirected Graph 中等

隐藏提示1

• Given n = 5 and edges = [[0, 1], [1, 2], [3, 4]], what should your return? Is this case a valid tree?

隐藏提示2

• According to the definition of tree on Wikipedia: “a tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.”

Condition

• graph must be connected
  • bfs result length = number of all nodes
• if graph has no cycle then it is tree
  • E <= V - 1
• corner case
  • if n == 1 and not edges: True

sol

class Solution:
    def validTree(self, n: int, edges: List[List[int]]) -> bool:
        if n == 1 and not edges:
            return True
        if n >= 2 and not edges:
            return False
        # must be V == E - 1
        if n - 1 != len(edges):
            return False
        
        node2Neighbors = collections.defaultdict(list)
        for edge in edges:
            node2Neighbors[edge[0]].append(edge[1])
            node2Neighbors[edge[1]].append(edge[0])
        
        startnode = edges[0][0]
        myqueue = collections.deque()
        myqueue.append(startnode)
        visited = set()
        while myqueue:
            currnode = myqueue.popleft()
            for neighbor in node2Neighbors[currnode]:
                if neighbor not in visited:
                    visited.add(neighbor)
                    myqueue.append(neighbor)
        if len(visited) == n: # include all nodes
            return True
        return False