第 12 章 生成对抗模型
作者: 张伟 (Charmve)
日期: 2021/05/19
- 第 12 章 生成对抗模型
- 12.1 Pixel RNN/CNN
- 12.2 自编码器 Auto-encoder
- 12.3 生成对抗网络 GAN
- 12.3.1 原理
- 12.3.2 项目实战
- 12.4 变分自编码器 Variational Auto-encoder, VAE
- 小结
- 参考文献
- 12.4.1 概述
- 12.4.2 基本原理
- 12.4.3 VAE v.s. AE 区别与联系
- 12.4.4 变分自编码器的代码实现
- 12.4.5 卷积变分自编码器的实现与简单应用
- 参考文献
- 附录: 图中英文翻译
变分自编码器(Variational auto-encoder,VAE)是一类重要的生成模型(generative model),在深度学习中占有重要地位,它最开始的目的是用于降维或特征学习。它于2013年由 Diederik P.Kingma 和Max Welling [1] 提出。2016年 Carl Doersch 写了一篇 VAEs 的 tutorial [2],对 VAEs 做了更详细的介绍,比文献[1]更易懂。VAE 模型与 GAN 相比,VAE 有更加完备的数学理论(引入了隐变量),理论推导更加显性,训练相对来说更加容易。
VAE 可以从神经网络的角度或者概率图模型的角度来解释,本文主要从概率图模型的角度尽量通俗地讲解其原理,并给出代码实现。
--> Back to Menu
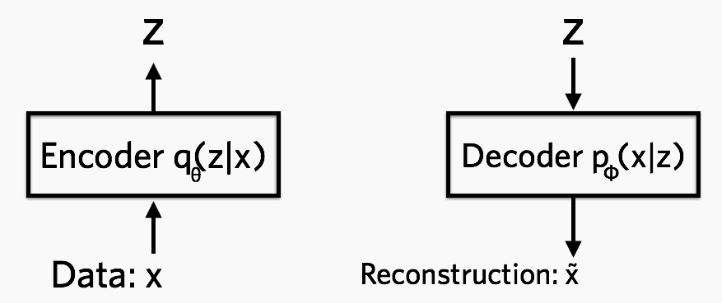
VAE 全名叫 变分自编码器,是从之前的 auto-encoder 演变过来的,auto-encoder 也就是自编码器,自编码器,顾名思义,就是可以自己对自己进行编码,重构。所以 AE 模型一般都由两部分的网络构成,一部分称为 encoder, 从一个高维的输入映射到一个低维的隐变量上,另外一部分称为 decoder, 从低维的隐变量再映射回高维的输入,如图12.1所示。
如上图所示,我们能观测到的数据是
简单而言,encoder 网络中的参数为
式(1)
上面的第一部分,可以看做是重建 loss,就是从
如果没有 KL 项,那 VAE 就退化成一个普通的 AE 模型,无法做生成,VAE 中的隐变量是一个分布,或者说近似高斯的分布,通过对这个概率分布采样,然后再通过 decoder 网络,VAE 可以生成不同的数据,这样VAE模型也可以被称为生成模型。
<你可能会问> 为什么叫变分自编码器?
推荐了解一下 变分推断,这里摘取其中某位大牛的回答:“简单易懂的理解变分其实就是一句话:用简单的分布q去近似复杂的分布p。” 所以暂时如果不考虑其他内容,联系一下整个 VAE 结构,应该就能懂变分过程具体是指什么了。 VAE 中的隐变量$z$ 的生成过程就是一个变分过程,我们希望用简单的$z$ 来映射复杂的分布,这既是一个降维的过程,同时也是一个变分推断的过程。
--> Back to Menu
理解变分自编码器的基本原理只需要关注整个模型的三个关键元素:
-
编码网络(Encoder Network),也称 推断网络 。该 NN 用来生成隐变量的参数(隐变量由多个高斯分布组成)。对于隐变量
$z$ ,首先初始化时可以是标准高斯分布,然后通过这个 NN,通过不断计算后验概率$q(z|x)$ 来逐步确定高斯分布的参数(均值和方差)。 - 隐变量(Latent Variable)。作为 Encoder 过程的产物,隐变量至少能够包含一些输入数据的信息(降维的作用),同时也应该具有生成类似数据的潜力。
- 解码网络(Decoder Network),也称 生成网络。该 NN 用于根据隐变量生成数据,我们希望它既有能力还原 encoder 的数据,同时还能根据数据特征生成一些输入样本中不包含的数据。
--> Back to Menu
该部分推导主要参考李宏毅老师的 课件视频
隐变量(Latent Variable)。上面已经讲过隐变量的基本概念,这里介绍隐变量在 VAE模型中的作用及特点。
- 隐变量
$z$ 是可以认为是隐藏层数据,它是不限定数目的符合 高斯分布 特征的数据。(根据实际情况确定数目) -
$z$ 由输入数据 X XX 的采样以及参数生成,它既包含$X$ 的信息(这个于 AutoEncoder 的隐藏层类似),同时也满足 高斯分布,方便接下来进行梯度下降或者其他优化技术 [1]。 - 隐变量的作用除了让生成网络尽可能还原原来的数据
$X$ ,同时也能生成原来数据中不存在的数据。
首先当我们引入隐变量
其中,用
如图12.2所示,标准的VAE模型是一个图模型,注意明显缺乏任何结构,甚至没有 “编码器” 路径:可以在不输入的情况下从模型中采样。这里,矩形是 “板符号”,这意味着我们可以在模型参数
上面也曾讲过,VAE 模型中同样有 Encoder 与 Decoder 过程,也就是说模型对于相同的输入时,也应该有尽可能相同的输出。所以这里再次遇到 Maximum likelihood(极大似然)。
在公式 (1) 中,将
式(2)
为了让公式 2 的输出极大似然
本步介绍的是如何实现与 AE 类似的功能,即保证输出数据极大似然与输入数据。
这里用到的网络称为 VAE 中的 生成网络,即根据隐变量
这个步骤需要确定隐变量
这里需要用到另外一个分布,$q(z|x)$ ,其中
同样地,这个任务也交给 NN 去完成。
这里的网络称为 推断网络。
这里对
式(3)
在公式3中,
为了让 Encode 过程也参与进来,这里引入
式(4)
然后,因为公式 $ \int_z{q(z|x)\log ({q(z|x)\over P(z|x)})} ,{\rm d}z
$ 即计算 KL 散度
所以公式4 一定大于等于
为了方便,我们把这个公式记作 $L_b$b ,(ELBO)
式(5)
根据公式 4 和公式 5,可以把
式(6)
这里首先需要提出一个重要结论:
log P(X) 值的大小与 q(z|x) 无关。所以不管怎么只调
所以可以通过调
调整的最终结果是使得
上面已经明确了目标:找到
公式推导如下: $$ L_b = \int_z{q(z|x)\log ({P(z,x)\over q(z|x)})} ,{\rm d}z \ \ \ \ \ \ \ \ \ \ \ \ \ = \int_z{q(z|x)\log ({P(x|z)P(z)\over q(z|x)})} ,{\rm d}z \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \int_z{q(z|x)\log ({P(z)\over q(z|x)})} ,{\rm d}z + \int_z{q(z|x)\log ({P(x|z)})} ,{\rm d}z \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = -KL(q(z|x)\ || \ P(z)) + \int_z{q(z|x)\log ({P(x|z)})} ,{\rm d}z $$
式(7)
公式中第2步到第3步的过程用到的是对数函数的性质,即 $$\log AB = \log A + \log B \$$
接下来需要 Minimize $ KL(q(z|x)\ || \ P(z))$,也就是调整$q(z|x)$ 来最小化,这里交给 NN 吧。
并且需要最大化另外一项,即$\int_z{q(z|x)\log ({P(x|z)})} ,{\rm d}z$,同样这份苦差事也交给 NN 去完成,如图12.6和12.7所示。
综合上面的推导,简单概括一下可以得到:
最终经过NN调参后,$KL(q(z|x)\ ||\ P(z|x))=0$ 在这里即 ELBO.
式(8)
接着对公式8进一步展开,可以得到
式(9)
公式 9 中的
在对应的代码实现中,有两种实现方式,一种是用公式 9 ,一种直接用公式 8。如果直接用公式 8 的话,可以理解为:$\log({P(x|z)})$ 在
--> Back to Menu
(1)区别
- VAE 中隐藏层服从高斯分布,AE 中的隐藏层无分布要求
- 训练时,AE 训练得到 Encoder 和 Decoder 模型,而 VAE 除了得到这两个模型,还获得了隐藏层的分布模型(即高斯分布的均值与方差)
- AE 只能重构输入数据X,而 VAE 可以生成含有输入数据某些特征与参数的新数据。
(2)联系
- VAE 与 AE 完全不同,但是从结构上看都含有 Decoder 和 Encoder 过程。
--> Back to Menu
如果只是基于 MLP 的VAE,就是普通的全连接网络:
import tensorflow as tf
from tensorflow.contrib import layers
## encoder 模块
def fc_encoder(x, latent_dim, activation=None):
e = layers.fully_connected(x, 500, scope='fc-01')
e = layers.fully_connected(e, 200, scope='fc-02')
output = layers.fully_connected(e, 2 * latent_dim, activation_fn=activation,
scope='fc-final')
return output
## decoder 模块
def fc_decoder(z, observation_dim, activation=tf.sigmoid):
x = layers.fully_connected(z, 200, scope='fc-01')
x = layers.fully_connected(x, 500, scope='fc-02')
output = layers.fully_connected(x, observation_dim, activation_fn=activation,
scope='fc-final')
return output关于这几个 loss 的计算:
## KL loss
def _kl_diagnormal_stdnormal(mu, log_var):
var = tf.exp(log_var)
kl = 0.5 * tf.reduce_sum(tf.square(mu) + var - 1. - log_var)
return kl
## 基于高斯分布的重建loss
def gaussian_log_likelihood(targets, mean, std):
se = 0.5 * tf.reduce_sum(tf.square(targets - mean)) / (2*tf.square(std)) + tf.log(std)
return se
## 基于伯努利分布的重建loss
def bernoulli_log_likelihood(targets, outputs, eps=1e-8):
log_like = -tf.reduce_sum(targets * tf.log(outputs + eps)
+ (1. - targets) * tf.log((1. - outputs) + eps))
return log_like可以看到,重建loss,如果是高斯分布,就是最小二乘,如果是伯努利分布,就是交叉熵,关于高斯分布的 KL loss 的详细推导,可以参考 KL散度的实战——1维高斯分布。
过程很复杂,结果很简单。如果有两个高斯分布 $\mathcal{N}1 \sim(\mu{1}, \sigma_{1}^{2})$,$\mathcal{N}2 \sim(\mu{2}, \sigma_{2}^{2})$,最后这两个分布的 KL 散度是:
式(10)
VAE 中,我们已经假设
式(11)
--> Back to Menu
本次实验采用的是 notebook,可以是自己电脑上安装的 jupyter notebook,也可以使用自己云服务器安装的,也可以考虑使用谷歌提供的 Colaboratory。
文件地址:/notebooks/chapter14_GAN/CVAE.ipynb
- 确定使用的是 tensorflow 2.x
!pip show tensorflow
如果当前安装的不是 tensorflow 2.x 的话,请输入以下命令安装:
!pip install tensorflow==2.3.0 -i https://pypi.tuna.tsinghua.edu.cn/simple
- 安装 imageio
!pip install imageio
import tensorflow as tf
import os
import time
import numpy as np
import glob
import matplotlib.pyplot as plt
import PIL
import imageio
from IPython import display
(train_images, _), (test_images, _) = tf.keras.datasets.mnist.load_data()
train_images = train_images.reshape(train_images.shape[0], 28, 28, 1).astype('float32')
test_images = test_images.reshape(test_images.shape[0], 28, 28, 1).astype('float32')
# 标准化图片到区间 [0., 1.] 内
train_images /= 255.
test_images /= 255.
# 二值化
train_images[train_images >= .5] = 1.
train_images[train_images < .5] = 0.
test_images[test_images >= .5] = 1.
test_images[test_images < .5] = 0.
# 使用 tf.data 来将数据分批和打乱
train_dataset = tf.data.Dataset.from_tensor_slices(train_images).shuffle(TRAIN_BUF).batch(BATCH_SIZE)
test_dataset = tf.data.Dataset.from_tensor_slices(test_images).shuffle(TEST_BUF).batch(BATCH_SIZE)准备工作做完了后,这里正式开始编写实现VAE模型。
训练过程中,为了生成样本
为了解决这个问题,我们使用了一个重新参数化的技巧。我们使用 decoder 参数和另一个参数
式(12)
其中
现在的
对于 VAE 模型构建,
- 在 Encoder NN中,使用两个卷积层和一个完全连接的层。、
- 在 Decoder NN中,通过使用一个完全连接的层和三个卷积转置层来镜像这种结构。 注意,在训练VAE时,通常避免使用批次标准化,因为使用小批量的额外随机性可能会加剧抽样随机性之外的不稳定性。
class CVAE(tf.keras.Model):
"""Convolutional variational autoencoder."""
def __init__(self, latent_dim):
super(CVAE, self).__init__()
self.latent_dim = latent_dim
self.encoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(28, 28, 1)),
tf.keras.layers.Conv2D(
filters=32, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Conv2D(
filters=64, kernel_size=3, strides=(2, 2), activation='relu'),
tf.keras.layers.Flatten(),
# No activation
tf.keras.layers.Dense(latent_dim + latent_dim),
]
)
self.decoder = tf.keras.Sequential(
[
tf.keras.layers.InputLayer(input_shape=(latent_dim,)),
tf.keras.layers.Dense(units=7*7*32, activation=tf.nn.relu),
tf.keras.layers.Reshape(target_shape=(7, 7, 32)),
tf.keras.layers.Conv2DTranspose(
filters=64, kernel_size=3, strides=2, padding='same',
activation='relu'),
tf.keras.layers.Conv2DTranspose(
filters=32, kernel_size=3, strides=2, padding='same',
activation='relu'),
# No activation
tf.keras.layers.Conv2DTranspose(
filters=1, kernel_size=3, strides=1, padding='same'),
]
)
@tf.function
def sample(self, eps=None):
if eps is None:
eps = tf.random.normal(shape=(100, self.latent_dim))
return self.decode(eps, apply_sigmoid=True)
def encode(self, x):
mean, logvar = tf.split(self.encoder(x), num_or_size_splits=2, axis=1)
return mean, logvar
def reparameterize(self, mean, logvar):
eps = tf.random.normal(shape=mean.shape)
return eps * tf.exp(logvar * .5) + mean
def decode(self, z, apply_sigmoid=False):
logits = self.decoder(z)
if apply_sigmoid:
probs = tf.sigmoid(logits)
return probs
return logits如上所述,VAE 通过
式(13)
实际操作中,我们优化了这种单样本蒙特卡罗估计:
式(14)
其中
optimizer = tf.keras.optimizers.Adam(1e-4)
def log_normal_pdf(sample, mean, logvar, raxis=1):
log2pi = tf.math.log(2. * np.pi)
return tf.reduce_sum(
-.5 * ((sample - mean) ** 2. * tf.exp(-logvar) + logvar + log2pi),
axis=raxis)
def compute_loss(model, x):
mean, logvar = model.encode(x)
z = model.reparameterize(mean, logvar)
x_logit = model.decode(z)
cross_ent = tf.nn.sigmoid_cross_entropy_with_logits(logits=x_logit, labels=x)
logpx_z = -tf.reduce_sum(cross_ent, axis=[1, 2, 3])
logpz = log_normal_pdf(z, 0., 0.)
logqz_x = log_normal_pdf(z, mean, logvar)
return -tf.reduce_mean(logpx_z + logpz - logqz_x)
@tf.function
def train_step(model, x, optimizer):
"""Executes one training step and returns the loss.
This function computes the loss and gradients, and uses the latter to
update the model's parameters.
"""
with tf.GradientTape() as tape:
loss = compute_loss(model, x)
gradients = tape.gradient(loss, model.trainable_variables)
optimizer.apply_gradients(zip(gradients, model.trainable_variables))(1) 训练
- 我们从迭代数据集开始。
- 在每次迭代期间,我们将图像传递给编码器,以获得近似后验
$q(z|x)$ 的一组均值和对数方差参数(log-variance parameters)。 - 然后,我们应用 重参数化技巧 从
$q(z|x)$ 中采样。 - 最后,我们将重新参数化的样本传递给解码器,以获取生成分布
$p(x|z)$ 的 logit。
注意: 由于我们使用的是由 keras 加载的数据集,其中训练集中有 6 万个数据点,测试集中有 1 万个数据点,因此我们在测试集上的最终 ELBO 略高于对 Larochelle 版 MNIST 使用动态二值化的文献中的报告结果。这里有个 关于 logits 的 解释。
(2) 生成图片
- 进行训练后,可以生成一些图片了。
- 我们首先从单位高斯先验分布
$p(z)$ 中采样一组潜在向量。 - 随后生成器将潜在样本
$z$ 转换为观测值的 logit,得到分布$p(x|z)$ 。 - 这里我们画出伯努利分布的概率。
epochs = 100
# set the dimensionality of the latent space to a plane for visualization later
latent_dim = 2
num_examples_to_generate = 16
# keeping the random vector constant for generation (prediction) so
# it will be easier to see the improvement.
random_vector_for_generation = tf.random.normal(
shape=[num_examples_to_generate, latent_dim])
model = CVAE(latent_dim)
def generate_and_save_images(model, epoch, test_sample):
mean, logvar = model.encode(test_sample)
z = model.reparameterize(mean, logvar)
predictions = model.sample(z)
fig = plt.figure(figsize=(4, 4))
for i in range(predictions.shape[0]):
plt.subplot(4, 4, i + 1)
plt.imshow(predictions[i, :, :, 0], cmap='gray')
plt.axis('off')
# tight_layout minimizes the overlap between 2 sub-plots
plt.savefig('image_at_epoch_{:04d}.png'.format(epoch))
plt.show()
# Pick a sample of the test set for generating output images
assert batch_size >= num_examples_to_generate
for test_batch in test_dataset.take(1):
test_sample = test_batch[0:num_examples_to_generate, :, :, :]
generate_and_save_images(model, 0, test_sample)
for epoch in range(1, epochs + 1):
start_time = time.time()
for train_x in train_dataset:
train_step(model, train_x, optimizer)
end_time = time.time()
loss = tf.keras.metrics.Mean()
for test_x in test_dataset:
loss(compute_loss(model, test_x))
elbo = -loss.result()
display.clear_output(wait=False)
print('Epoch: {}, Test set ELBO: {}, time elapse for current epoch: {}'
.format(epoch, elbo, end_time - start_time))
generate_and_save_images(model, epoch, test_sample)一百次循环后,生成的图片如下图 12.8 所示。
同时可以生成 gif 图片来方便查看生成过程,如图12.9所示。
anim_file = 'cvae.gif'
with imageio.get_writer(anim_file, mode='I') as writer:
filenames = glob.glob('image*.png')
filenames = sorted(filenames)
for filename in filenames:
image = imageio.imread(filename)
writer.append_data(image)
image = imageio.imread(filename)
writer.append_data(image)展示 gif 图片
import tensorflow_docs.vis.embed as embed
embed.embed_file(anim_file)最终生成的过度图像如下图 12.10 所示。
扩展阅读 - VAE均值与方差的故事
很久以前,有个叫VAE的生产车间,车间主任雇佣了$\mu$ 与$\sigma$ 。两个小伙,但并没有直接给他们安排工作任务,只告诉他们:好好干,如果你们做得不好,那就扣你们的工资。
刚开始。$\mu$ 与$\sigma$ 有些懵逼:连任务都不说清楚,就叫我们好好干?
第一天扣的工资最多,因为懵逼了一天。
第二天俩小伙对车间生产流程,生产目标熟悉了,扣得少了一些。
第三天他们更加谨慎了,毕竟谁都害怕扣工资,就这么点钱。
第四天、第五天......后来$\mu$ 和$\sigma$ 都摸清楚了套路,懂得怎么增加收入。
终于有一天车间主任满意了,看着漂漂亮亮的产品,决定给$\mu$ 和$\sigma$ 评职称。众所周知,评上职称的工资一般都比较高。
最终被评为"车间最优均值"称号。
那$\sigma$ 最终是不是就被评为"车间最美方差"呢?不是的,他被评为"车间最美标准差''。后来他们这个生产小组被评为''正态分布",再后来车间主任用同样的手段忽悠更多的无业游民(随机数),通过很多次勤奋工作与调整(训练),组成一组又一组"正态分布"(隐变量)。
从此,VAE车间的萨与$\sigma$ 勤勤恳恳干活,为 VAE 车间创造了很多产品,为大家所喜爱,而他们在车间勤奋努力不断调整自己的故事,也一时传为佳话。
--> Back to Menu
[1] Kingma D P, Welling M. Auto-Encoding Variational Bayes[J]. stat, 2014, 1050: 10.
[2] DOERSCH C. Tutorial on Variational Autoencoders[J]. stat, 2016, 1050: 13.
[3] Blei, David M., "Variational Inference." Lecture from Princeton, https://www.cs.princeton.edu/courses/archive/fall11/cos597C/lectures/variational-inference-i.pdf.
[4] VAE 模型基本原理简单介绍 https://blog.csdn.net/smileyan9/article/details/107362252
[5] 机器学习:VAE(Variational Autoencoder) 模型 https://blog.csdn.net/matrix_space/article/details/83683811
[6] TensorFlow. Convolutional Variational Autoencoder. https://tensorflow.google.cn/tutorials/generative/cvae
| 图序号 | 英文原文 | 中文翻译 |
|---|---|---|
| 图12.3 | Maximizing Likelihood | 最大似然估计 |
| P(z) 是正态分布,μ(z), o(z) 是将被估计的参数 | ||
| Maximizing the likelihood of the observed x | 最大化x的似然估计 | |
| Tunning the parameters to maximize likelihood L | 调整参数以使似然L最大化 | |
| We need another distribution q(z|x) | 我们需要另外一个分布 q(z|x) | |
| \ | \ | \ |
| 图12.4 | Maximizing Likelihood | 最大似然估计 |
| q(z|x) can be any distribution | q(z|x)可以是任何一种分布 | |
| lower bound Lb | 取 Lb 的下界 | |
| \ | \ | \ |
| 图12.5 | Maximizing Likelihood | 最大似然估计 |
| Find P(x|z) and q(z|x) maximizing Lb | 寻找 P(x|z) 和 q(z|x) 使得 Lb 最大 | |
| q(z|x) will be an approximation of p(z|x) in the end | q(z|x) 最终将会被 p(z|x) 近似化 | |
| \ | \ | \ |
| 图12.7 | Connection with network | 连接网络 |
| Refer to the Appendix B of the original VAE paper | 请参考附件B中的论文原文 | |
| this is the auto-encoder | 这就是自编码器 |